题目内容
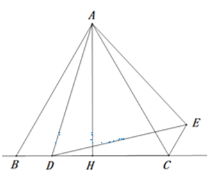
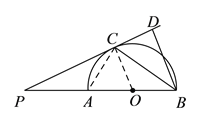
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上 一点,
延长线上 一点, ![]() 是⊙
是⊙![]() 的切线,切点为
的切线,切点为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .求证:
.求证:
(![]() )
)![]() .
.
(![]() )
)![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)连接OC,由PC为⊙![]() 的切线,利用切线的性质得到OC⊥PC,再由BD⊥PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;
的切线,利用切线的性质得到OC⊥PC,再由BD⊥PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;
(2)连接AC,由AB为⊙![]() 的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到△ABC与△CBD相似,利用相似三角形对应边成比例,变形即可得证.
的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到△ABC与△CBD相似,利用相似三角形对应边成比例,变形即可得证.
证明:(![]() )连接
)连接![]() ,
,
∵![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(![]() )连接
)连接![]() ,
,
∵![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
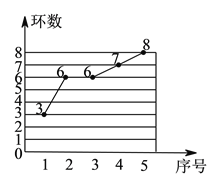
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.