题目内容
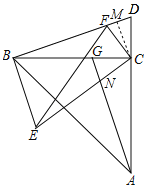
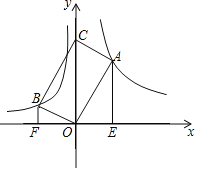
【题目】如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为___;BE长为____.
【答案】1:5, ![]() .
.
【解析】
作CM⊥DF于M,则∠CMD=90°,由已知得出∠BCD=∠ACB=90°,AC=BC,BC=3CD,求出CD=1,AC=BC=3,证明△CDM∽△BDC,![]() ,得出
,得出![]() ,证明△AGC≌△BDC,得出∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,得出△CDF的面积=2△CDM的面积,求出△CFD的面积:△ECF的面积=1:5;证明△ACN≌△BCF,得出AN=BF,CN=CF=CD=CG=1,GN=DF,证明△CGN∽△CBE,得出
,证明△AGC≌△BDC,得出∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,得出△CDF的面积=2△CDM的面积,求出△CFD的面积:△ECF的面积=1:5;证明△ACN≌△BCF,得出AN=BF,CN=CF=CD=CG=1,GN=DF,证明△CGN∽△CBE,得出![]() ,在Rt△DCM中,求出DM=
,在Rt△DCM中,求出DM=![]() ,得出DF=2DM=
,得出DF=2DM=![]() ,代入计算即可.
,代入计算即可.
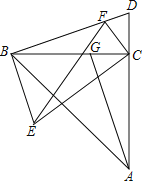
作CM⊥DF于M,如图所示:
则∠CMD=90°,
∵在△ABD中,BC为AD边上的高线,tan∠BAD=1,
∴∠BCD=∠ACB=90°,AC=BC,
在Rt△BCD中,∵tanD=3=![]() ,
,
∴BC=3CD,
∵AD=AC+CD=BC+CD=4,
∴CD=1,AC=BC=3,
∵∠CMD=∠BCD,∠D=∠D,
∴△CDM∽△BDC, ![]() ,
,
∴![]() ,
,
在△AGC和△BDC中,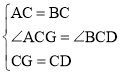 ,
,
∴△AGC≌△BDC(SAS),
∴∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,
由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,
∴△CDF的面积=2△CDM的面积,
∴△CFD的面积:△ECF的面积=1:5;
∵CG=CD,
∴CG=CF,
在△ACN和△BCF中,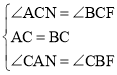 ,
,
∴△ACN≌△BCF(ASA),
∴AN=BF,CN=CF=CD=CG=1,
∴GN=DF,BC:CG=CE:CN,
∵∠GCN=∠BCE,
∴△CGN∽△CBE,
∴![]() ,
,
在Rt△DCM中,tanD=3,CD=1,
∴DM=![]() ,
,
∵CD=CF,CM⊥DF,
∴DF=2DM=![]() ,
,
∴GN=![]() ,
,
∴![]() =
=![]() ,
,
解得:BE=![]() ;
;
故答案为:1:5,![]() .
.