Question

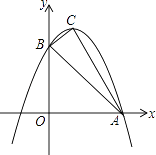
【题目】如图1，已知五边形OABCD的顶点O在坐标原点，点A在y轴上，点D在x轴上，AB∥x轴，CD∥y轴，动点P从点O出发，以每秒1单位的速度，沿五边形OABCD的边顺时针运动一周，顺次连结P，O，A三点所围成图形的面积为S，点P的运动时间为t秒，S与t之间的函数关系如图2中折线OEFGHI所示．

（1）求证：AB=2；

（2）求五边形OABCD的面积．

（3）求直线BC的函数表达式；

（4）若直线OP把五边形OABCD的面积分成1：3两部分，求点P的坐标．

Answer 1

【答案】（1）详见解析；（2）24；（3）y=﹣x+；（4）点P（）或（）．

【解析】

（1）先判断出OA=6，再利用三角形ABO的面积即可求出AB；

（2）先判断出BC，CD，进而求出B'D，再用面积的和即可得出结论；

（3）先确定出点B，C坐标，利用待定系数法即可得出结论；

（4）先判断出点P必在线段BC上，进而求出求出三角形ABM的面积，再分两种情况利用面积建立方程求解即可得出结论．

（1）连接OB，由图1，图2知，OA=6，

当点P运动到点B时，S△AOP=S△AOB=×6×AB=6，

∴AB=2，

（2）由（1）知AB=2，

∴OA+AB=6+2=8，

∴图2中的a是8秒，

由图1，图2知，当点P从B运动到点C时，用了13﹣8=5秒钟，

∴BC=5，

点P从点C运动到点D时，△AOP的面积不变，用了15﹣13=2秒，

∴CD=2，

过点B作BB'⊥OD于B'，

∴四边形OABB'是矩形，BB'=OA=6，OB'=AB=2，

过点C作CC'⊥BB'于B'，

∴四边形CC'B'D是矩形，B'C'=CD=2，DB'=CC'

∴BC'=BB'﹣B'C'=4

在Rt△BC'C中，根据勾股定理得，CC'==3，

∴DB'=3，

∴OD=OB'+DB'=2+2=5，

∴S五边形OABCD的面积=S矩形AOBB'+S梯形CDB'B=2×6+（2+6）×3=24；

（3）由（2）知，BB'=6，OB'=2，

∴B（2，6），

由（2）知，CD=2，OD=5，

∴C（5，2），

设直线BC的解析式为y=kx+b'，

∴，

∴，

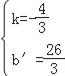∴直线BC的解析式为y=﹣x+；

（4）如图3，

连接OB，OC，由图2知，S△AOB=6，

由（2）知，CD=2，OD=5，

∴S△COD=5，

延长CB交y轴于M，

∴M（0，），

∴AM=，

∴S△AMB=AM×AB=

由（2）知，S五边形OABCD的面积=24，

∴点P必在线段BC上，

设P（m，﹣ m+）（0＜m＜5），

∵直线OP把五边形OABCD的面积分成1：3两部分，

∴S四边形OABP=S五边形OABCD的面积=8或S四边形OABP=S五边形OABCD的面积=16，

当S四边形OABP=8时，∴S△OPM=S四边形OABP+S△AMB==××m，

∴m=，

∴P（，）

当S四边形OABP'=16时，S△OP'M=S四边形OABP'+S△AMB==××m，

∴m=，

∴P'（，），

即：满足题意的点P（，）或（，）．