题目内容
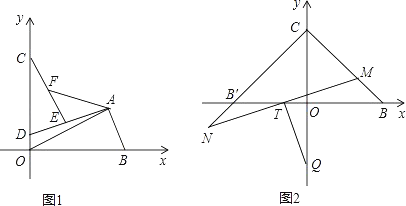
【题目】如图,直角坐标系中,点B(a,0),点C(0,b),点A在第一象限.若a,b满足(a﹣t)2+|b﹣t|=0(t>0).
(1)证明:OB=OC.
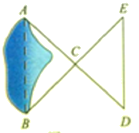
(2)如图1,连接AB,过A作AD⊥AB交y轴于D,在射线AD上截取AE=AB,连接CE,F是CE的中点,连接AF,OA,当点A在第一象限内运动(AD不过点C)时,证明:∠OAF的大小不变.
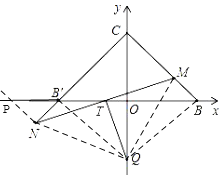
(3)如图2,B′与B关于y轴对称,M在线段BC上,N在CB′的延长线上,且BM=NB′,连接MN交x轴于点T,过T作TQ⊥MN交y轴于点Q,求点Q的坐标.
【答案】(1)证明见解析;(2)证明见解析;(3)Q(0,-t).
【解析】
(1)利用平方和绝对值的非负数性质即可用t表示出a、b,即可得B、C坐标,进而可得答案;(2)如图,延长AF到点P,使PF=AF;连接CP、OP、OF,利用SAS可证明△AEF≌△PCF,可得AE=PC=AB,∠AEF=∠PCF,AE∥PC,由平行线的性质可得∠PCO=∠CDA=180-∠ADO,利用四边形内角和可得∠ABO=180-∠ADO,即可证明∠PCO=∠ABO,利用SAS可证明△PCO≌△ABO,可得OP=OA,∠POC=∠AOB,利用角的和差关系可得∠AOP=∠BOC=90°,即可证明△AOP为等腰直角三角形,可得∠OAF=45°,是定值;(3)过N作NP∥MB,交x轴于P;连接NQ、MQ、BQ、B′Q,由轴对称性质可得BB′=2OB,BC=B′C,可得△BCB′是等腰直角三角形,根据等腰直角三角形的性质及平行线的性质可得∠B′PN=∠PB′N,即可证明NP=NB′=MB,利用AAS可证明△PTN≌△BTM,可得NT=MT,利用SSS可证明△BQM≌△B′QN,可得∠NB′Q=∠MBQ,利用SAS可证明△BCQ≌△B′CQ,可得△OBQ为等腰直角三角形,可得OQ=OB,即可求出Q点坐标.
(1)∵(a-t)≥0,|b-t|≥0,
∴a-t=0,b-t=0,
解得:a=t,b=t
∴B(t,0)、C(0,t)
∴OB=OC
(2)如图,延长AF到点P,使PF=AF;连接CP、OP、OF,
在△AEF和△PCF中,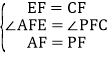
∴△AEF≌△PCF,
∴AE=PC=AB,∠AEF=∠PCF
∴AE∥PC,∠PCO=∠CDA=180-∠ADO
四边形ABOD中,∠ABO=360-∠BOD-∠BAD-∠ADO,
∵∠BOD=90°,AD⊥AB,
∴∠ABO=180-∠ADO,
∴∠PCO=∠ABO
在△PCO和△ABO中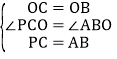 ,
,
∴△PCO≌△ABO,
∴OP=OA,∠POC=∠AOB
∴∠AOP=∠BOC-∠AOB+∠POC=∠BOC=90°,
∴△AOP为等腰直角三角形,
∴∠OAF=45°,是定值,不发生改变.
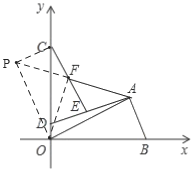
(3)过N作NP∥MB,交X轴于P;连接NQ、MQ、BQ、B′Q,
由(1)得△BOC是等腰直角三角形
∵B、B′关于y轴对称,
∴BB′=2OB,BC=B′C,
∴△BCB′是等腰直角三角形,∠BB′C=∠B′BC=45°,
∵NP∥MB,
∴∠B′PN=∠B′BC=45°,
∵∠PB′N=∠BB′C=45°,
∴∠B′PN=∠PB′N,
∴NP=NB′=MB
在△PTN和△BTM中,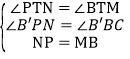 ,
,
∴△PTN≌△BTM,NT=MT,T为MN中点,
∵QT⊥MN,
∴QT为MN垂直平分线,
∴MQ=NQ
∵B、B′关于y轴对称,Q在y轴上,
∴BQ=B′Q
在△BQM≌△B′QN中,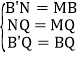 ,
,
∴△BQM≌△B′QN(SSS),
∴∠NB′Q=∠MBQ,
在△BCQ和△B′CQ中,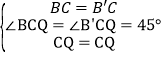
∴△BCQ≌△B′CQ,
∴∠MBQ=∠CB′Q=∠NB′Q,
∵∠CB′Q+∠NB′Q=180°,
∴∠NB′Q=∠MBQ=90°,
∴∠OBQ=45°,
∴△OBQ为等腰直角三角形,
∴OQ=OB=t
∴Q(0,-t).