题目内容
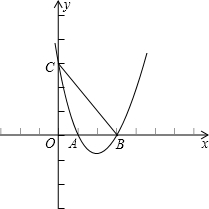
如图,在平面直角坐标系中,点A的坐标为(7,0),点B的坐标为(3,4),
(1)求经过O、A、B三点的抛物线解析式;
(2)将线段AB绕A点顺时针旋转75°至AC,直接写出点C的坐标;
(3)在y轴上找一点P,第一象限找一点Q,使得以O、B、Q、P为顶点的四边形是菱形,求出点Q的坐标;
(4)△OAB的边OB上有一动点M,过M作MN∥OA交AB于N,将△BMN沿MN翻折得△DMN.设MN=x,△DMN与△OAB重叠部分的面积为y,求出y与x之间的函数关系式,并求出重叠部分面积的最大值.
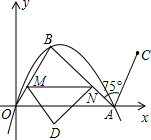
(1)求经过O、A、B三点的抛物线解析式;
(2)将线段AB绕A点顺时针旋转75°至AC,直接写出点C的坐标;
(3)在y轴上找一点P,第一象限找一点Q,使得以O、B、Q、P为顶点的四边形是菱形,求出点Q的坐标;
(4)△OAB的边OB上有一动点M,过M作MN∥OA交AB于N,将△BMN沿MN翻折得△DMN.设MN=x,△DMN与△OAB重叠部分的面积为y,求出y与x之间的函数关系式,并求出重叠部分面积的最大值.

(1)设抛物线解析式为y=ax2+bx(a≠0),
∵点A(7,0)、B(3,4)在抛物线上,
∴
,
解得
,
∴抛物线解析式y=-
x2+
x;
(2)过点C作CE⊥x轴于E,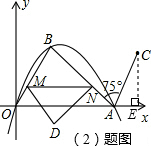
∵A(7,0),B(3,4),
∴AB=
=4
,∠BAO=45°,
∵AB绕A点顺时针旋转75°至AC,
∴∠CAE=180°-45°-75°=60°,
∴CE=4
×
=2
,AE=4
×
=2
,
∴OE=OA+AE=7+2
,
∵点C在第一象限,
∴点C的坐标为(7+2
,2
);
(3)由勾股定理得,OB=
=5,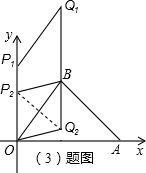
①OB是菱形的边时,点Q到x轴的距离为4+5=9,
所以,点Q的坐标(3,9);
②OB是菱形的对角线时,BQ=
OB÷cos∠OBQ=
÷
=
,
所以,点Q到x轴的距离为4-
=
,
所以,点Q的坐标为(3,
),
综上所述,以O、B、Q、P为顶点的四边形是菱形,点Q的坐标为(3,9)或(3,
);
(4)当点D在OA上时,MN=
OA=
,
①0<x≤
时,重叠部分是△DMN的面积,
△OAB的面积=
×7×4=14,
∵MN∥OA,
∴△BMN∽△BOA,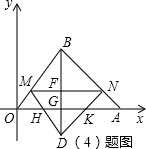
∴
=(
)2=(
)2=
x2,
∴y=
x2•14=
x2,
当x=
时,y最大且最大值为
;
②
<x<7时,连接BD交MN于F,交OA于G,设DM与OA相交于H,DN与OA相交于K,
由△BMN∽BOA得,
=
,
即
=
,
解得BF=
x,
由翻折的性质得,BF=DF=
x,
∴FG=4-
x,DG=
x-(4-
x)=
x-4,
由△DHK∽△DMN得,
=
,
即
=
,
解得HK=2x-7,
重叠部分面积y=S四边形MHKN=
×(2x-7+x)×(4-
x)=-
x2+8x-14,
配方得,y=-
(x-
)2+
,
当x=
时,y最大且最大值为
,
综上所述,y与x之间的函数关系式为y=
,
∵
<
,
∴当x=
时,y最大且最大值为
.
∵点A(7,0)、B(3,4)在抛物线上,
∴
|
解得
|
∴抛物线解析式y=-
| 1 |
| 3 |
| 7 |
| 3 |
(2)过点C作CE⊥x轴于E,

∵A(7,0),B(3,4),
∴AB=
| (7-3)2+42 |
| 2 |
∵AB绕A点顺时针旋转75°至AC,
∴∠CAE=180°-45°-75°=60°,
∴CE=4
| 2 |
| ||
| 2 |
| 6 |
| 2 |
| 1 |
| 2 |
| 2 |
∴OE=OA+AE=7+2
| 2 |
∵点C在第一象限,
∴点C的坐标为(7+2
| 2 |
| 6 |
(3)由勾股定理得,OB=
| 32+42 |

①OB是菱形的边时,点Q到x轴的距离为4+5=9,
所以,点Q的坐标(3,9);
②OB是菱形的对角线时,BQ=
| 1 |
| 2 |
| 5 |
| 2 |
| 4 |
| 5 |
| 25 |
| 8 |
所以,点Q到x轴的距离为4-
| 25 |
| 8 |
| 7 |
| 8 |
所以,点Q的坐标为(3,
| 7 |
| 8 |
综上所述,以O、B、Q、P为顶点的四边形是菱形,点Q的坐标为(3,9)或(3,
| 7 |
| 8 |
(4)当点D在OA上时,MN=
| 1 |
| 2 |
| 7 |
| 2 |
①0<x≤
| 7 |
| 2 |
△OAB的面积=
| 1 |
| 2 |
∵MN∥OA,
∴△BMN∽△BOA,

∴
| S△BMN |
| S△BOA |
| MN |
| OA |
| x |
| 7 |
| 1 |
| 49 |
∴y=
| 1 |
| 49 |
| 2 |
| 7 |
当x=
| 7 |
| 2 |
| 7 |
| 2 |
②
| 7 |
| 2 |
由△BMN∽BOA得,
| MN |
| OA |
| BF |
| BG |
即
| x |
| 7 |
| BF |
| 4 |
解得BF=
| 4 |
| 7 |
由翻折的性质得,BF=DF=
| 4 |
| 7 |
∴FG=4-
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 8 |
| 7 |
由△DHK∽△DMN得,
| HK |
| MN |
| DG |
| DF |
即
| HK |
| x |
| ||
|
解得HK=2x-7,
重叠部分面积y=S四边形MHKN=
| 1 |
| 2 |
| 4 |
| 7 |
| 6 |
| 7 |
配方得,y=-
| 6 |
| 7 |
| 14 |
| 3 |
| 14 |
| 3 |
当x=
| 14 |
| 3 |
| 14 |
| 3 |
综上所述,y与x之间的函数关系式为y=
|
∵
| 7 |
| 2 |
| 14 |
| 3 |
∴当x=
| 14 |
| 3 |
| 14 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
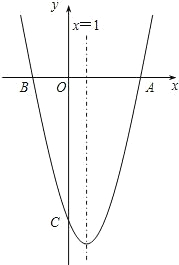 段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.
段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1. 点在直线BC上.
点在直线BC上.
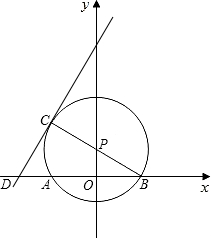 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为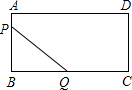 就停止移动.据此解答下列问题:
就停止移动.据此解答下列问题: