题目内容
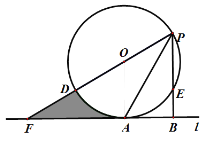
【题目】如图,⊙O的直径PD=8,点E是⊙O上一点,点A是![]() 的中点,连接PA,过点A作直线l⊥PE,垂足为点B,PB=6,直径PD的延长线交直线l于点F.
的中点,连接PA,过点A作直线l⊥PE,垂足为点B,PB=6,直径PD的延长线交直线l于点F.
(1)求证:直线l是⊙O的切线;
(2)求线段PA的长;
(3)求阴影部分的面积.
【答案】(1)见解析;(2)AP=![]() ;(3)
;(3)![]()
【解析】
(1)连接OA,由等弧对等角可得∠APD=∠APE,再由等边对等角得∠APD=∠OAP,然后推出OA∥BP进而得出OA⊥BF,即可得证;
(2)连接AD,由圆周角定理可得∠DAP=90°,然后易证△DAP∽△APB,由比例关系求出AP;
(3)利用勾股定理求出AD,可知△OAD为等边三角形,然后根据![]() 即可得出答案.
即可得出答案.
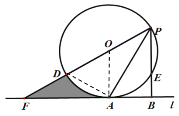
解:(1)证明:如图,连接OA.
![]()
![]() ,
,
∴∠APD=∠APE,
∵OA=OP,
∴∠APD=∠OAP,
∴∠OAP=∠APE,
∴OA∥BP,
∵PB⊥FB,
∴OA⊥BF,
∴直线l是⊙O的切线.
(2)如图,连接AD,
∵AD是⊙O的直径
∴∠DAP=∠ABP=90°
又∵∠APD=∠APE,
∴△DAP∽△APB,
∴AP2=PB·PD,
∴AP=![]() .
.
(3)∵AD=![]()
∴AD=OD=OA
∴△OAD是等边三角形,
∴∠AOD=60°
∴![]()
∴![]() .
.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2﹣bx+c的y与x的部分对立值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论①抛物线的开口向下:②其图象的对称轴为x=1:③当x<1时.函数值y随x的增大而增大,④方程ax2+bx+c=0有一个根大于4.其中正确的结论有_____