题目内容
如图,抛物线的顶点坐标为M(1,4),与x轴的一个交点是A(-1,0),与y轴交于点B,直线x=1交x轴于点N.(1)求抛物线的解析式及点B的坐标;
(2)求经过B、M两点的直线的解析式,并求出此直线与x轴的交点C的坐标;
(3)若点P在抛物线的对称轴x=1上运动,请你探索:在x轴上方是否存在这样的P点,使
 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)设抛物线的解析式是y=a(x-1)2+4,将A(-1,0)点坐标代入解析式即可,然后令x=0即可求出点B的坐标;
(2)设直线BM的解析式为y=kx+b,将BM两点坐标代入y=kx+b即可求得直线的解析式,令y=0即可求出点C的坐标;
(3)连接PA,过点P作PQ⊥BM,根据三角形相似的性质列出关于m的方程,解方程得出符合条件的解即使点P的坐标.
(2)设直线BM的解析式为y=kx+b,将BM两点坐标代入y=kx+b即可求得直线的解析式,令y=0即可求出点C的坐标;
(3)连接PA,过点P作PQ⊥BM,根据三角形相似的性质列出关于m的方程,解方程得出符合条件的解即使点P的坐标.
解答:解:(1)∵抛物线的顶点坐标为(1,4)
∴设抛物线的解析式是y=a(x-1)2+4
把A点坐标x=-1,y=0代入,得0=a(-1-1)2+4,
∴a=-1
∴抛物线的解析式是y=-(x-1)2+4
即y=-x2+2x+3
令x=0,得y=3,
∴B点的坐标是(0,3);
(2)设直线BM的解析式为y=kx+b,
把x=0,y=3;x=1,y=(4分)别代入,得
,
解得:
,
∴直线BM的解析式是y=x+3,
令y=0.得0=x+3,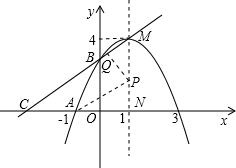
∴x=-3,
∴C点坐标是(-3,0);
(3)假设存在满足题意的点P(1,m),其中m>0.
连接PA,则PA是⊙P的半径.
在Rt△PAN中,PA=
=
,
过点P作PQ⊥BM,垂足为Q.
则PQ=PA时,⊙P与直线BM相切.
在Rt△MPQ和Rt△MCN,sin∠CMN=
=
,
∴
=
,
整理,得m2+8m-8=0,
解这个方程,得m1=-4+2
,m2=-4-2
(,舍去)
∴存在满足题意的点P,其坐标为(1,-4+2
).
∴设抛物线的解析式是y=a(x-1)2+4
把A点坐标x=-1,y=0代入,得0=a(-1-1)2+4,
∴a=-1
∴抛物线的解析式是y=-(x-1)2+4
即y=-x2+2x+3
令x=0,得y=3,
∴B点的坐标是(0,3);
(2)设直线BM的解析式为y=kx+b,
把x=0,y=3;x=1,y=(4分)别代入,得
|
解得:
|
∴直线BM的解析式是y=x+3,
令y=0.得0=x+3,

∴x=-3,
∴C点坐标是(-3,0);
(3)假设存在满足题意的点P(1,m),其中m>0.
连接PA,则PA是⊙P的半径.
在Rt△PAN中,PA=
| m2+22 |
| m2+4 |
过点P作PQ⊥BM,垂足为Q.
则PQ=PA时,⊙P与直线BM相切.
在Rt△MPQ和Rt△MCN,sin∠CMN=
| PQ |
| PM |
| CN |
| CM |
∴
| ||
| 4-m |
| 4 | ||
4
|
整理,得m2+8m-8=0,
解这个方程,得m1=-4+2
| 6 |
| 6 |
∴存在满足题意的点P,其坐标为(1,-4+2
| 6 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和三角形的相似及动点问题等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
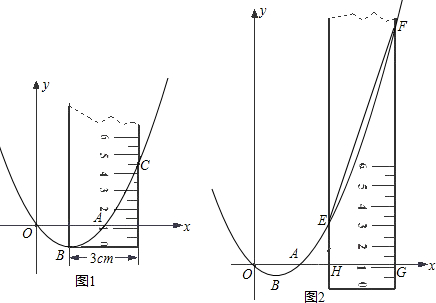
 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
