Question

在平面直角坐标系中，将一块腰长为2

2

cm的等腰直角三角板ABC如图放置，BC边与x轴重合，∠ACB=90°，直角顶点C的坐标为（-3，0）．
（1）点A的坐标为

（-3，2

2

）

，点B的坐为

(-3-2

2

，0)

；
（2）求以原点O为顶点且过点A的抛物线的解析式；
（3）现三角板ABC以1cm/s的速度沿x轴正方向平移，则平移的时间为多少秒时，三角板的边所在直线与半径为2cm的⊙O相切？

Answer 1

分析：（1）根据等腰直角三角形的腰长求得AC和BC的长，然后根据点C的坐标求得两点的坐标即可；
（2）设抛物线的解析式为y=ax²，将点A的坐标代入即可求得抛物线的解析式；
（3）随着三角形的运动分四种情况：①当三角板向右平移1cm时，AC与圆相切，②当三角板向右平移3cm时，AB与半圆相切，③当三角板向右平移5cm时，边AC与⊙O第二次相切，④当三角板向右平移，边AB所在直线与⊙O第二次相切．分别求得半圆的圆心移动的距离后，再求得运动的时间．

解答：解：（1）∵AC=BC=2

2

，直角顶点C的坐标为（-3，0），
∴点A的坐标为（-3，2

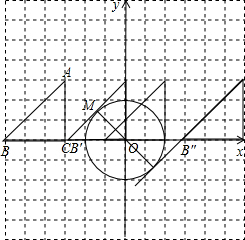
2

），
点B的坐标为(-3-2

2

，0)；
（2）∵抛物线的顶点为原点，
∴设抛物线y=ax²，
∵抛物线经过点A，
∴9a=2

2

，
解得：a=

2 2

9

∴抛物线的解析式为：y=

2 2

9

x²          
（3）①当三角板向右平移1cm时，AC与⊙O第一次相切，t₁=1s
②当三角板向右平移3cm时，边AB与⊙O第一次相切，
设切点为M，在Rt△OMB’中OM=2，∠OB′P=45°，
∴OB′=

22+22

=2

2

∴BB′=OB-OB′=(2

2

+3)-2

2

=3
∴t₂=3s
③当三角板向右平移5cm时，边AC与⊙O第二次相切，t₃=5s
④当三角板向右平移，边AB所在直线与⊙O第二次相切，设切点为P，在Rt△OPB″中
OP=2，∠OB″P=45°，
∴OB″=

22+22

=2

2

∴BB″=(2

2

+3)+2

2

=4

2

+3
∴t4=4

2

+3s
所以  t₁=1s   或 t₂=3s   或  t₃=5s 或 t4=4

2

+3s

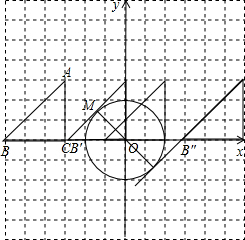
点评：本题考查了圆的综合知识，要求学生熟练掌握圆与直线的位置关系，并结合常见的函数进行综合分析，考查了学生数形结合的分析能力．