题目内容
【题目】请在横线上填上合适的内容，完成下面的证明：
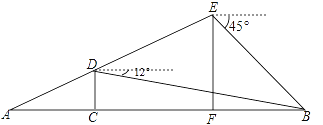
如图，射线AH交折线ACGFEN于点B、D、E．已知∠A=∠1，∠C=∠F，BM平分∠CBD，EN平分∠FEH．求证：∠2=∠3．
证明：∵∠A=∠1（已知）
∴AC∥GF（ ）
∴（ ）（ ）
∵∠C=∠F（已知）
∴∠F=∠G
∴（ ）（ ）
∴（ ）（ ）
∵BM平分∠CBD，EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
【答案】见解析.
【解析】
依据平行线的判定以及性质，即可得到∠C＝∠G，即可得到∠F＝∠G，进而判定CG∥EF，再根据平行线的性质，即可得到∠CBD＝∠FEH，依据角平分线的定义，即可得出结论．
∵∠A=∠1(已知)，
∴AC∥GF(内错角相等，两直线平行)，
∴∠C=∠G(两直线平行，内错角相等)，
∵∠C=∠F(已知)，
∴∠F=∠G，
∴CG∥EF(内错角相等，两直线平行)，
∴∠CBD=∠FEH(两直线平行，同位角相等)，
∵BM平分∠CBD，EN平分∠FEH，
∴∠2=
∠CBD，∠3=∠FEH，
∴∠2=∠3，
故答案为：内错角相等，两直线平行，∠C=∠G，两直线平行，内错角相等，CG∥EF，内错角相等，两直线平行，∠CBD=∠FEH，两直线平行，同位角相等，∠CBD，∠FEH．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
