题目内容
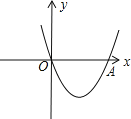
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧)
(1)当a=﹣1时,求A,B两点的坐标;
(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.当a=2时,求PB+PC的值.
【答案】(1)A(﹣2,0),B(0,0).(2)14.
【解析】
(1)把a=﹣1代入得y=﹣x2﹣2x,令y=0,得:﹣x2﹣2x=0,解得x1,x2,根据点A在点B的左侧,则可求出两点坐标;
(2)当a=2时,有y=2x2﹣2x,令y=0,得2x2﹣2x=0,解得x1=0,x2=1,根据点A在点B的左侧,则A(0,0),B(1,0),可得PB=2;当x=3时,![]() ,则可求出PB+PC=14;
,则可求出PB+PC=14;
解:(1)当a=﹣1时,有y=﹣x2﹣2x.
令y=0,得:﹣x2﹣2x=0.
解得x1=0,x2=﹣2.
∵点A在点B的左侧,
∴A(﹣2,0),B(0,0);
(2)当a=2时,有y=2x2﹣2x.
令y=0,得2x2﹣2x=0.
解得x1=0,x2=1.
∵点A在点B的左侧,
∴A(0,0),B(1,0).
∴PB=2,
当x=3时,![]() ,
,
∴PC=12.
∴PB+PC=14.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).