题目内容
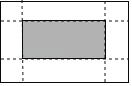
【题目】如图，在平行四边形ABCD中，AE：EB=1:2，DE交于点F.
（1）求AE：DC的值.
（2）△AEF与△CDF相似吗？若相似，求出相似比，请说明理由.
（3）如果
，求
.
【答案】（1）AE∶DC=1∶3；（2）相似，相似比：1∶3（3）
【解析】
（1）由比例的性质可得AE∶AB=1∶3，再由平行四边形对边相等得DC=AB，所以AE∶DC=1∶3；
（2）由平行四边形对边平行，得两组内错角相等，即可判定相似，相似比= AE∶DC=1∶3；
（3）由相似三角形的面积比等于相似比的平方可求出
.
（1）∵AE：EB=1:2
∴AE∶AB=1∶3
∵四边形ABCD为平行四边形
∴DC=AB
∴AE∶DC=1∶3
（2）∵四边形ABCD为平行四边形
∴DC∥AB
∴∠EAF=∠DCF，∠AEF=∠CDF
∴△AEF∽△CDF
∴相似比= AE∶DC=1∶3
故△AEF与△CDF相似，相似比为1∶3.
（3）∵△AEF∽△CDF
∴
练习册系列答案
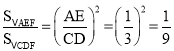
备战中考寒假系列答案
相关题目
