题目内容
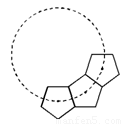
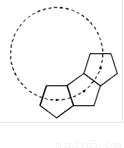
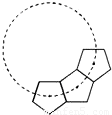
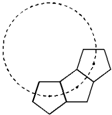如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需（ ）个五边形．分析：先根据多边形的内角和公式（n-2）•180°求出正五边形的每一个内角的度数，再延长五边形的两边相交于一点，并根据四边形的内角和求出这个角的度数，然后根据周角等于360°求出完成这一圆环需要的正五边形的个数，然后减去3即可得解．
解答：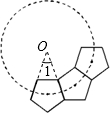
解：五边形的内角和为（5-2）•180°=540°，
所以正五边形的每一个内角为540°÷5=108°，
如图，延长正五边形的两边相交于点O，则∠1=360°-108°×3=360°-324°=36°，
360°÷36°=10，
∵已经有3个五边形，
∴10-3=7，
即完成这一圆环还需7个五边形．
故选B．
解：五边形的内角和为（5-2）•180°=540°，所以正五边形的每一个内角为540°÷5=108°，
如图，延长正五边形的两边相交于点O，则∠1=360°-108°×3=360°-324°=36°，
360°÷36°=10，
∵已经有3个五边形，
∴10-3=7，
即完成这一圆环还需7个五边形．
故选B．
点评：本题考查了多边形的内角和公式，延长正五边形的两边相交于一点，并求出这个角的度数是解题的关键，注意需要减去已有的3个正五边形．
练习册系列答案
相关题目
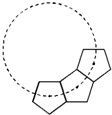18、如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需
