题目内容
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论k取不为1的任何值方程总有两个不相等的实数根.
(2)设![]() 是该方程的两个实数根,记
是该方程的两个实数根,记![]() ,
,![]() 的值能为1吗?若能,求出此时
的值能为1吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)见详解;(2)不能,见详解
【解析】
(1)利用根的判别式公式代入△=b2-4ac即可;
(2)先由根与系数关系 分别表示出x1+x2与x1x2的值,然后将代入S=x12+x22-x1x2表示为k的代数式,最后化简变形为关于k的一元二次方程进行判断即可.
解:(1)证明:△=b2-4ac=(2k)2-4(k-1)×2=4k2-8k+8=4(k2-2k)+8=4(k2-2k+1-1)+8=4(k-1)2+12,
∵4(k-1)2≥0,
∴4(k-1)2+12>0,
∴无论k取不为1的任何值,方程总有两个不相等的实数根;
(2)由根与系数关系有
![]()
∴![]()
化简得: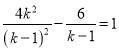
方程两边同时乘以(k-1)2得,![]() 即
即![]() ,
,
∵△=(-4)2-4×3×5<0.
∴方程无解,
∴S=x12+x22-x1x2的值不能为1.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3