题目内容
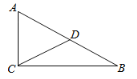
【题目】如图,Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=__________.
【答案】6或![]()
【解析】
由Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,即可求得AB与CD的值,又由以D、C、P为顶点的三角形与△ABC相似,可得∠DPC=90°或∠CDP=90°,然后根据相似三角形的对应边成比例,即可求得PC的值.
∵Rt△ABC中,∠ACB=90°,AC=9,BC=12,
∴AB=15,
∵D是AB边的中点,
∴CD=BD=![]() AB=7.5,
AB=7.5,
∵以D、C、P为顶点的三角形与△ABC相似,
∴∠DPC=90°或∠CDP=90°,
(1)如图1:
若∠DPC=90°,则DP∥AC,
∴![]() =
=![]() =
=![]() ,
,
∴BP=![]() BC=6,
BC=6,
则PC=6;
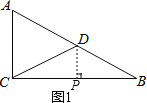
(2)如图2:
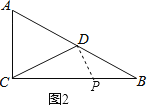
若∠CDP=90°,则△CDP∽△BCA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴PC=![]() .
.
综上所述:PC=6或![]() .
.
故答案为:6或![]() .
.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目