题目内容
【题目】如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.
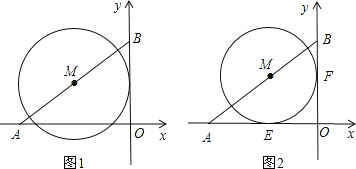
(1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由;
(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.
【答案】(1)直线OB与⊙M相切.;(2)M的坐标为(-![]() ,
,![]() ).
).
【解析】
试题(1)设线段OB的中点为D,证明MD=4,且MD⊥OB即可;
(2)先利用待定系数法求得直线AB的解析式:![]() ,根据切线的性质得到点M到x轴、y轴的距离都相等,设M(a,-a)(-8<a<0).代入
,根据切线的性质得到点M到x轴、y轴的距离都相等,设M(a,-a)(-8<a<0).代入![]() ,即可求得a的值,即得到M的坐标.
,即可求得a的值,即得到M的坐标.
试题解析:(1)直线OB与⊙M相切.
理由:
设线段OB的中点为D,连结MD.
因为点M是线段AB的中点,所以MD∥AO,MD=4.
所以∠AOB=∠MDB=900,
所以MD⊥OB,点D在⊙M上.
又因为点D在直线OB上,
所以直线OB与⊙M相切.
(2)可求得过点A、B的一次函数关系式是![]() ,
,
因为⊙M与x轴、y轴都相切,
所以点M到x轴、y轴的距离都相等.
设M(a,-a) (-8<a<0) .
把x=a,y=-a代入![]() ,
,
得-a=![]() a+6,得a=-
a+6,得a=-![]() .
.
所以点M的坐标为(-![]() ,
,![]() ).
).

练习册系列答案
相关题目