题目内容
【题目】如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为1cm2，则它移动的距离AA′等于（ ）
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
【答案】B
【解析】试题分析：根据平移的性质，结合阴影部分是平行四边形，△AA′H与HCB′都是等腰直角三角形，则设AA′=x，则阴影部分底边长为x，高A′D=2-x，根据平行四边形的面积公式即可列出方程求解．
试题解析：设AC交A′B′于H，如图
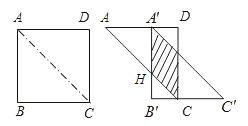
∵∠A=45°，∠D=90°，
∴△AA′H是等腰直角三角形，
设AA′=x，则阴影部分底边长为x，高A′D=2-x，
∴x×(2-x)=1
∴x=1
即AA′=1cm．
故选B．
练习册系列答案
相关题目
【题目】如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．
1 | ° | x | 7 | ﹣3 | … |
（1）可知x= ，= ，°= ；
（2）试判断第2016个格子中的数是多少？并给出相应的理由．
（3）判断：前n个格子中所填整数之和是否可能为2016？若能，求出n的值，若不能，请说明理由．
