题目内容
【题目】解答题
（1）问题发现
如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：
①∠ACE的度数为；
②线段AC、CD、CE之间的数量关系为 ．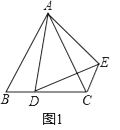 
（2）拓展探究
如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．
（3）解决问题
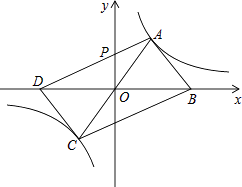
如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．
【答案】
（1）60°；AC=CD+CE
（2）
解：∠ACE=45°， 
AC=CD+CE，理由是：
如图2，∵△ABC和△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，
∴AB=AC，AD=AE，∠BAC﹣∠DAC=∠DAE﹣∠DAC，
即∠BAD=∠CAE，
∴△ABD≌△ACE，
∴BD=CE，∠ACE=∠B=45°，
∵BC=CD+BD，
∴BC=CD+CE，
∵在等腰直角三角形ABC中，BC= AC，
∴ AC=CD+CE；
（3）
解：如图3，过A作AC的垂线，交CB的延长线于点F，
∵∠BAD=∠BCD=90°，AB=AD=2，CD=1，
∴BD=2 ，BC= 
，
∵∠BAD=∠BCD=90°，
∴∠BAD+∠BCD=180°，
∴A、B、C、D四点共圆，
∴∠ADB=∠ACB=45°，
∴△ACF是等腰直角三角形，
由（2）得： AC=BC+CD，
∴AC= 
= 
= 
．
【解析】解：（1）①∵△ABC和△ADE均为等边三角形，
∴AB=AC，AD=AE，∠BAC=∠DAE=∠B=60°，
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，
即∠BAD=∠CAE，
∴△BAD≌△CAE（SAS），
∴∠ACE=∠B=60°，
所以答案是：60°；②线段AC、CD、CE之间的数量关系为：AC=CD+CE；
理由是：由①得：△BAD≌△CAE，
∴BD=CE，
∵AC=BC=BD+CD，
∴AC=CD+CE；
所以答案是：AC=CD+CE；
