题目内容
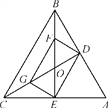
【题目】已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点，连接DF，FG，EG，DE，求证：DF＝EG.
【答案】证明见解析.
【解析】试题分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC，DE=
BC，FG∥BC，FG=
BC，从而得到DE∥FG且DE=FG，再根据一组对边平行且相等的四边形是平行四边形判断出四边形DEGF是平行四边形，然后根据平行四边形的对边相等证明即可．
试题解析：
证明：由题意得点E，D分别是AC，AB的中点，
∴ED是△ABC的中位线．∴ED
BC.
∵F，G分别是BO，CO的中点，
∴FG是△OBC的中位线．
∴FG
BC.
∴EDFG.
∴四边形EDFG是平行四边形．
∴DF＝EG.
练习册系列答案
阅读快车系列答案
相关题目
