题目内容
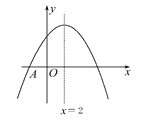
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0),顶点坐标为(2,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①当x>6时,y<0;②5a+b>0;③![]() ≤a≤-
≤a≤-![]() ,④4≤n<5中,正确有( )
,④4≤n<5中,正确有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】根据抛物线的对称性,由点A的坐标(-2,0)和对称轴x=2,得到与x轴的另一个交点为(6,0),然后根据图像可知当x>6时,y<0,故①正确;
根据图示知,抛物线开口方向向下,则a<0.由对称轴x=![]() =2,解得b=-4a,所以5a+b=5a-4a=a<0,即5a+b<0.故②错误;
=2,解得b=-4a,所以5a+b=5a-4a=a<0,即5a+b<0.故②错误;
根据抛物线与y轴的交点在(0,3),(0,4)之间(包含端点),可得3≤c≤4,令x=-2,则4a-2b+c=0,又由于b=-4a,可得c=-12a,即3≤-12a≤4,解得-![]() ≤a≤-
≤a≤-![]() ,故③正确;
,故③正确;
根据抛物线的顶点坐标为(![]() ,
,![]() ),可得n=
),可得n=![]() =c-
=c-![]() ,然后根据b=-4a,3≤c≤4,-
,然后根据b=-4a,3≤c≤4,-![]() ≤a≤-
≤a≤-![]() ,可得n=c-4a,即4≤n≤
,可得n=c-4a,即4≤n≤![]() ,故④不正确.
,故④不正确.
故选:B.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
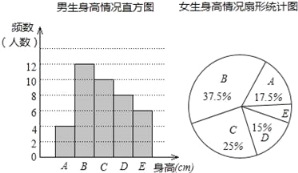
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<160 |
B | 160≤x<165 |
C | 165≤x<170 |
D | 170≤x<175 |
E | x≥175 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?