Question

【题目】在直角坐标平面内，已知点，将点向右平移5个单位得到点

(1)描出点的位置，并求的面积．

(2)若在轴下方有一点，使，写出一个满足条件的点的坐标．并指出满足条件的点有什么特征．

Answer 1

【答案】（1）10；（2），这些点在轴下方，与轴平行且与轴距离为的一条直线上

【解析】

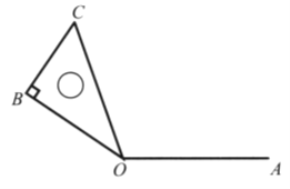
（1）根据已知点的坐标得出A，B的位置，再利用点B向右平移5个单位得到点C，即可得出C点坐标；再根据B、C两点的坐标得出BC的长，从而求出的面积

（2）根据和BC的长得出高的长，从而求出D点坐标，再根据同底等高的三角形的面积相等得出点D的特征

解：（1）∵点向右平移5个单位得到点C，

∴点的坐标为,

的位置如图所示

∵，,

∴，

∵，

∴

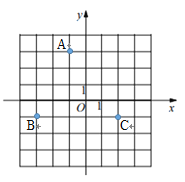
（2）设三角形BCD的高为h，∵，

∴

∴h=2

∵点在轴下方，

∴；

∵同底等高的三角形的面积相等；

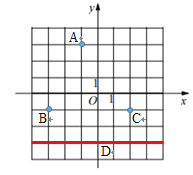
∴这些点D在轴下方,与轴平行且与轴距离为的一条直线上