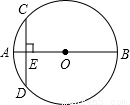
题目内容
 如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2
如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2 .
.
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为________.
解:(1)∵AB为⊙O的直径,弦CD⊥AB于E,
∴弧BC=弧BD,
∴∠BDC= ∠BOD,
∠BOD,
而∠CDB=15°,
∴∠BOD=2×15°=30°,
在Rt△ODE中,∠DOE=30°,OE=2 ,
,
∴OE= DE,OD=2DE,
DE,OD=2DE,
∴DE=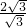 =2,
=2,
∴OD=4,
即⊙O的半径为4;
(2)有4种情况:如图:




①如图1所示:∵OA=OB,∠AOB=30°,
∴∠OAB=∠OBA=75°,
∵CD⊥AB,AB是直径,
∴弧BC=弧BD,
∴∠CAB= ∠BOD=15°,
∠BOD=15°,
∴∠CAB=∠BAO+∠CAB=15°+75°=90°;
②如图2所示,∠CAD=75°-15°=60°;
③如图3所示:∠ACB=90°;
④如图4所示:∠ACB=60°;
故答案为:60°或90°.
分析:(1)求出∠BOD的度数,在Rt△ODE中,根据∠DOE=30°,OE=2 ,求出DE和OD即可;
,求出DE和OD即可;
(2)分为4种情况,分别求出∠CAB和∠OAB(或∠OAD、∠OCB)的度数,相加(或相减)即可求出答案.
点评:本题考查了圆周角定理及其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半;直径所对的圆周角为直角.也考查了垂径定理以及角平分线的定义,本题是一道比较容易出错的题目,注意不能漏解啊.
∴弧BC=弧BD,
∴∠BDC=
 ∠BOD,
∠BOD,而∠CDB=15°,
∴∠BOD=2×15°=30°,
在Rt△ODE中,∠DOE=30°,OE=2
 ,
,∴OE=
 DE,OD=2DE,
DE,OD=2DE,∴DE=
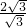 =2,
=2,∴OD=4,
即⊙O的半径为4;
(2)有4种情况:如图:




①如图1所示:∵OA=OB,∠AOB=30°,
∴∠OAB=∠OBA=75°,
∵CD⊥AB,AB是直径,
∴弧BC=弧BD,
∴∠CAB=
 ∠BOD=15°,
∠BOD=15°,∴∠CAB=∠BAO+∠CAB=15°+75°=90°;
②如图2所示,∠CAD=75°-15°=60°;
③如图3所示:∠ACB=90°;
④如图4所示:∠ACB=60°;
故答案为:60°或90°.
分析:(1)求出∠BOD的度数,在Rt△ODE中,根据∠DOE=30°,OE=2
 ,求出DE和OD即可;
,求出DE和OD即可;(2)分为4种情况,分别求出∠CAB和∠OAB(或∠OAD、∠OCB)的度数,相加(或相减)即可求出答案.
点评:本题考查了圆周角定理及其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半;直径所对的圆周角为直角.也考查了垂径定理以及角平分线的定义,本题是一道比较容易出错的题目,注意不能漏解啊.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
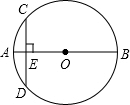 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
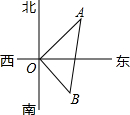 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
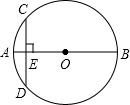 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为