题目内容
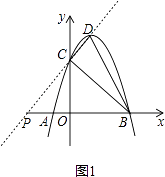
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
【答案】
(1)0,3,1,4
(2)解:∵在三角形中两边之差小于第三边,
∴延长DC交x轴于点P,
设直线DC的解析式为y=kx+b,把D、C两点坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线DC的解析式为y=x+3,
将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,
如图1,点P(﹣3,0)即为所求;
(3)解:过点C作CE∥x,交直线BD于点E,如图2,

由(2)得直线DC的解析式为y=x+3,
可求得直线BD的解析式为y=﹣2x+6,直线BC的解析式为y=﹣x+3,
在y=﹣2x+6中,当y=3时,x= ![]() ,
,
∴E点坐标为( ![]() ,3),
,3),
设直线P′C′与直线BC交于点M,
∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),
∴直线P′C′的解析式为y=x+3﹣t,
联立 ![]() ,解得
,解得 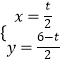 ,
,
∴点M坐标为( ![]() ,
, ![]() ),
),
∵B′C′∥BC,B′坐标为(3+t,0),
∴直线B′C′的解析式为y=﹣x+3+t,
分两种情况讨论:
①当0<t< ![]() 时,如图2,B′C′与BD交于点N,
时,如图2,B′C′与BD交于点N,
联立 ![]() ,解得
,解得 ![]() ,
,
∴N点坐标为(3﹣t,2t),
S=S△B′C′P﹣S△BMP﹣S△BNB′= ![]() ×6×3﹣
×6×3﹣ ![]() (6﹣t)×
(6﹣t)× ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() t×2t=﹣
t×2t=﹣ ![]() t2+3t,
t2+3t,
其对称轴为t= ![]() ,可知当0<t<
,可知当0<t< ![]() 时,S随t的增大而增大,当t=
时,S随t的增大而增大,当t= ![]() 时,有最大值
时,有最大值 ![]() ;
;
②当 ![]() ≤t<6时,如图3,直线P′C′与DB交于点N,
≤t<6时,如图3,直线P′C′与DB交于点N,
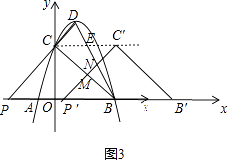
联立 ![]() ,解得
,解得 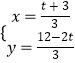 ,
,
∴N点坐标为( ![]() ,
, ![]() ),
),
S=S△BNP′﹣S△BMP′= ![]() (6﹣t)×
(6﹣t)× ![]() ﹣
﹣ ![]() ×(6﹣t)×
×(6﹣t)× ![]() =
= ![]() (6﹣t)2=
(6﹣t)2= ![]() t2﹣t+3;
t2﹣t+3;
显然当 ![]() <t<6时,S随t的增大而减小,当t=
<t<6时,S随t的增大而减小,当t= ![]() 时,S=
时,S= ![]()
综上所述,S与t之间的关系式为S=  ,且当t=
,且当t= ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]() .
.
【解析】解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴C(0,3),D(1,4),
所以答案是:0;3;1;4;

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案