题目内容
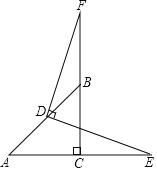
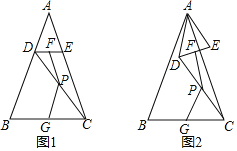
【题目】如图1，在△ABC中，AB＝AC，∠BAC＝α，点D、E分别在边AB、AC上，AD＝AE，连接DC，点F、P、G分别为DE、DC、BC的中点．
（1）观察猜想：图1中，线段PF与PG的数量关系是 ，∠FPG＝ （用含α的代数式表示）
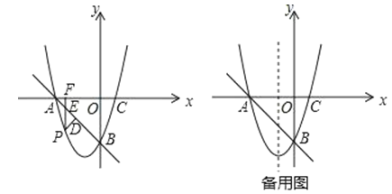
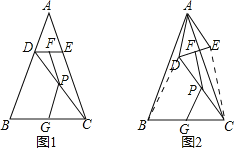
（2）探究证明：当△ADE绕点A旋转到如图2所示的位置时，小新猜想（1）中的结论仍然成立，请你证明小新的猜想．
（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝2，AB＝6，请直接写出PF的最大值．
【答案】（1）PF＝PG，180°﹣α；（2）∠FPG＝180°﹣α；证明见解析；（3）PF的最大值为4．
【解析】
（1）根据等腰三角形的性质和三角形的中位线定理解答即可；
（2）连接BD，CE，利用全等三角形的判定和性质以及三角形中位线定理解答；
（3）当EC最大时，FP最大，进而解答即可．
（1）如图1，∵在△ABC中，AB＝AC，∠BAC＝α，点D、E分别在边AB、AC上，AD＝AE，
∴AB﹣AD＝AC﹣AE，
即DB＝CE，
∵点F、P、G分别为DE、DC、BC的中点，
∴PF＝
CE，PG＝BD，
∴PF＝PG，
∵点F、P、G分别为DE、DC、BC的中点，
∴PG∥BD，PF∥CE，
∴∠PGC＝∠DBC，∠DPF＝∠DCE，
∴∠FPG＝∠DPF+∠DPG
＝∠DCE+∠PGC+∠DCB
＝∠ACD+∠ACE+∠DBC+∠DCB
＝∠ACD+∠ABD+∠DBC+∠DCB
＝∠ABC+∠ACB，
∵∠ABC+∠ACB＝180°﹣∠BAC
∴∠FPG＝180°﹣α；
故答案为PF＝PG，180°﹣α；
（2）如图2，连接BD，CE，由题意知AB＝AC，∠BAD＝∠CAE，AD＝AE，
∴△ABD≌△ACE（SAS），
∴BD＝CE，∠ABD＝∠ACE，
∵点F、P、G分别为DE、DC、BC的中点，
∴PF，PG分别是△CDE和△CDB的中位线，
∴PG∥BD，PF∥CE，
∴∠PGC＝∠DBC，∠DPF＝∠DCE，
∴∠FPG＝∠DPF+∠DPG
＝∠DCE+∠PGC+∠DCB
＝∠ACD+∠ACE+∠DBC+∠DCB
＝∠ACD+∠ABD+∠DBC+∠DCB
＝∠ABC+∠ACB，
∵∠ABC+∠ACB＝180°﹣∠BAC
∴∠FPG＝180°﹣α；
（3）当EC最大时，FP最大，EC的最大值为AE+AC＝8，
∴PF＝EC，即PF的最大值为4．
