题目内容
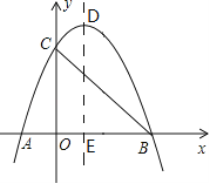
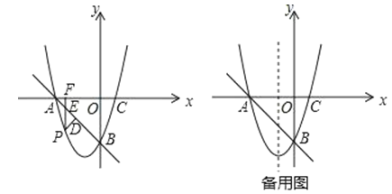
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,C(1,0),与y轴交于点B(0,﹣3).
(1)求抛物线的解析式;
(2)点P是直线AB下方的抛物线上一动点,过点P作x轴的垂线,垂足为点F,交直线AB于点E,作PD⊥AB于点D.当△PDE的周长最大时,求出点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)P(-![]() ,-
,-![]() ).
).
【解析】
(1)根据待定系数法即可求解;
(2)先求出点A的坐标,得出∠AEF=45°,再根据![]() ,可得△PDE是等腰直角三角形,从而得到△PDE的周长与PE的关系式,可知PE最大时,△PDE的周长最大,设点F的横坐标为m,将PE用含m的式子表示,最后根据二次函数的性质即可求解.
,可得△PDE是等腰直角三角形,从而得到△PDE的周长与PE的关系式,可知PE最大时,△PDE的周长最大,设点F的横坐标为m,将PE用含m的式子表示,最后根据二次函数的性质即可求解.
(1)∵抛物线y=x2+bx+c经过点B(0,﹣3),C(1,0),
∴c=-3,1+b+c=0,
解得:b=2,c=-3,
∴抛物线的解析式为:y=x2+2x﹣3;
(2)在y=x2+2x﹣3中,y=0时,x1=1,x2=﹣3,
∴A(﹣3,0),
∵B(0,-3),
∴OA=OB=3,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=45°,
可得△PDE是等腰直角三角形,
由A(﹣3,0),B(0,3)得直线AB的解析式为:y=-x-3,
C△PDE=PE+PD+DP
=PE+![]() PE+
PE+![]() PE
PE
=(![]() +1)PE,
+1)PE,
设P(m,m2+2m﹣3),则E(m,-m-3),PE=-m2-3m
C△PDE=(![]() +1)(-m2-3m)
+1)(-m2-3m)
=-(![]() +1)(m+
+1)(m+![]() )2+
)2+![]() (
(![]() +1),
+1),
∴当m=-![]() 时,△PDE的周长越大,此时P点坐标为(-
时,△PDE的周长越大,此时P点坐标为(-![]() ,-
,-![]() ).
).

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目