题目内容
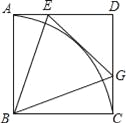
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

【答案】(1)见解析;(2)α,β之间的数量关系式为2α+β=60°.
【解析】
(1)根据三角形的中位线的性质得到EF=![]() CD,根据直角三角形的性质得到AE=
CD,根据直角三角形的性质得到AE=![]() BD,于是得到结论;
BD,于是得到结论;
(2)根据题意得到△AEF是等边三角形,求得∠AEF=60°,根据三角形中位线的性质和三角形外角的性质即可得到结论.
(1)∵点E、F分别为DB、BC的中点,
∴EF=![]() CD,
CD,
∵∠DAB=90°,
∴AE=![]() BD,
BD,
∵DB=DC,
∴AE=EF;
(2)∵AF=AE,AE=EF,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵∠DAB=90°,点E、F分别为DB、BC的中点,
∴AE=DE,EF∥CD,
∴∠ADE=∠DAE=α,∠BEF=∠BDC=β,
∴∠AEB=2∠ADE=2α,
∴∠AEF=∠AEB+∠FEB=2α+β=60°,
∴α,β之间的数量关系式为2α+β=60°.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目