题目内容
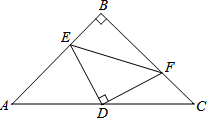 如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,
如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,(1)试说明DE=DF;
(2)求EF长.
分析:(1)连结BD,根据等腰三角形的性质可以得出∠ABD=∠CBD=45°,再证明△BED≌△CFD就可以得出结论;
(2)由△BED≌△CFD可以得出BE=CF,就可以求出BF的值,在Rt△BEF中,由勾股定理就可以求出结论.
(2)由△BED≌△CFD可以得出BE=CF,就可以求出BF的值,在Rt△BEF中,由勾股定理就可以求出结论.
解答:解:(1)证明:连结BD,
∵AB=AC,∠ABC=90°,
∴∠B=∠C=45°.
∵D是AC的中点,
∴BD=AD=CD=
AC,∠ABD=∠CBD=45°,BD⊥AC,
∴∠ABD=∠C,∠BDC=90°,
即∠CDF+∠BDF=90°.
∵DE⊥DF,
∴∠EDF=90°.
即∠EDB+∠BDF=90°,
∴∠EDB=∠CDF.
在△BED和△CFD中
,
∴△BED≌△CFD(ASA),
∴DE=DF.
(2)∵△BED≌△CFD,
∴BE=CF.
∵AB=AE+BE,
∴AB=AE+CF.
∵AE=12,FC=5,
∴AB=17,
∴BF=12.
在Rt△EBF中,由勾股定理,得
EF=13.
答:EF=13.
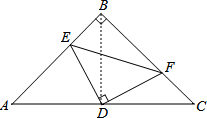
∵AB=AC,∠ABC=90°,
∴∠B=∠C=45°.
∵D是AC的中点,
∴BD=AD=CD=
| 1 |
| 2 |
∴∠ABD=∠C,∠BDC=90°,
即∠CDF+∠BDF=90°.
∵DE⊥DF,
∴∠EDF=90°.
即∠EDB+∠BDF=90°,
∴∠EDB=∠CDF.
在△BED和△CFD中
|
∴△BED≌△CFD(ASA),
∴DE=DF.
(2)∵△BED≌△CFD,
∴BE=CF.
∵AB=AE+BE,
∴AB=AE+CF.
∵AE=12,FC=5,
∴AB=17,
∴BF=12.
在Rt△EBF中,由勾股定理,得
EF=13.
答:EF=13.

点评:本题考查了等腰直角三角形的性质的运用,全等三角形的判定与性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
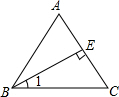 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
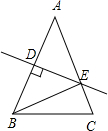 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=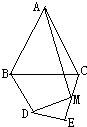 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.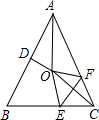 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是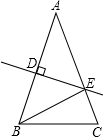 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是