题目内容
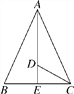
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)问t为何值时,PA=PB?
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
【答案】(1)当t=![]() 或13s时PA=PB;(2)当t=6s或13s或12s或 10.8s 时,△BCP为等腰三角形;(3)当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.
或13s时PA=PB;(2)当t=6s或13s或12s或 10.8s 时,△BCP为等腰三角形;(3)当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.
【解析】
(1)分两种情况:点P在AC上和点P在AB上,分别根据移动的路程,求得时间t的值即可;
(2)分两种情况:①若P在边AC上时,BC=CP=6cm,此时用的时间为6s;②若P在AB边上时,有三种可能:i若使BP=CB=6cm,此时AP=4cm,P运动的路程为4+8=12cm,用的时间为12时;ii)若CP=BC=6cm,过C作CD⊥AB于点D,根据面积法求得高CD=4.8cm,求出BP=2PD=7.2cm,得出P运动的路程为18-7.2=10.8cm,即可得出结果;ⅲ)若BP=CP,则∠PCB=∠B,证出PA=PC得出PA=PB=5cm,得出P的路程为13cm,即可得出结果;
(3)分两种情况:①当P、Q没相遇前:P点走过的路程为t,Q走过的路程为2t,根据题意得出方程,解方程即可;②当P、Q没相遇后:当P点在AB上,Q在AC上,则AP=t-8,AQ=2t-16,根据题意得出方程,解方程即可;即可得出结果.
解:(1)如图2,作AB的垂直平分线DE,交AB于E,交AC于D,连接DB,
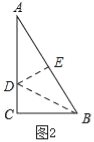
则DA=DB,EA=EB,
∵△ABC中,∠C=90°,AB=10cm,BC=6cm,
∴AC=![]() =8cm,
=8cm,
①当点P与点D重合时,PA=PB,
此时,CP=1t=t,AP=8﹣t=BP,
∴在Rt△BCP中,t2+62=(8﹣t)2,
解得t=![]() ;
;
②当点P与点E重合时,PA=PB,
此时,PA=PB=![]() AB=5,
AB=5,
∴CA+AP=13,即1t=13,
解得t=13,
故当t=![]() 或13s时,△BCP为等腰三角形;
或13s时,△BCP为等腰三角形;
(2)如图3,若P在边AC上时,BC=CP=6cm,
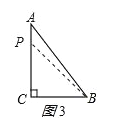
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有三种情况:
①如图4,若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
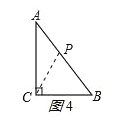
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②如图5,若CP=BC=6cm,过C作斜边AB的高,
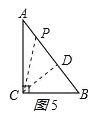
根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③如图6,若BP=CP时,则∠PCB=∠PBC,

∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,
∴∠ACP=∠CAP,
∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴当t=6s或13s或12s或 10.8s 时,△BCP为等腰三角形;
(3)分两种情况:①当P、Q没相遇前:如图7,
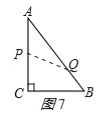
P点走过的路程为tcm,Q走过的路程为2tcm,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t=12,
∴t=4s;
②当P、Q相遇后:如图8,
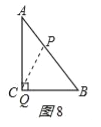
当P点在AB上,Q在AC上,则AP=t﹣8,AQ=2t﹣16,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t﹣8+2t﹣16=12,
∴t=12s,
故当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】上网流量、语音通话是手机通信消费的两大主体,目前,某通信公司推出消费优惠新招﹣﹣“定制套餐”,消费者可根据实际情况自由定制每月上网流量与语音通话时间,并按照二者的阶梯资费标准缴纳通信费.下表是流量与语音的阶梯定价标准.
流量阶梯定价标准 | |
使用范围 | 阶梯单价(元/MB) |
1﹣100MB | a |
101﹣500MB | 0.07 |
501﹣20GB | b |
语音阶梯定价标准 | |
使用范围 | 阶梯资费(元/分钟) |
1﹣500分钟 | 0.15 |
501﹣1000分钟 | 0.12 |
1001﹣2000分钟 | m |
【小提示:阶梯定价收费计算方法,如600分钟语音通话费=0.15×500+0.12×(600﹣500)=87元】
(1)甲定制了600MB的月流量,花费48元;乙定制了2GB的月流量,花费120.4元,求a,b的值.(注:1GB=1024MB)
(2)甲的套餐费用为199元,其中含600MB的月流量;丙的套餐费用为244.2元,其中包含1GB的月流量,二人均定制了超过1000分钟的每月通话时间,并且丙的语音通话时间比甲多300分钟,求m的值.