Question

【题目】如图（1），在中，，．点为内一点，且．

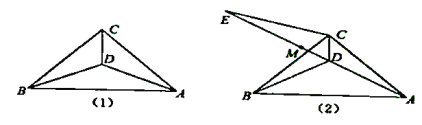
（1）求证：；

（2），为延长线上的一点，且．如图（2），

①求证：平分；

②若点在线段上，且，请判断、的数量关系，并给出证明．

Answer 1

【答案】（1）见详解；（2）①见详解；②ME=BD，理由见详解.

【解析】

（1）利用线段的垂直平分线的性质即可证明；

（2）①易证BD=AD，可得△ADC≌△BDC，即可求得∠ACD=∠BCD=45°即可解题；

②连接MC，易证△MCD为等边三角形，即可证明△BDC≌△EMC即可解题；

（1）证明：∵CB=CA，DB=DA，

∴CD垂直平分线段AB，

∴CD⊥AB．

（2）①证明：∵AC=BC，

∴∠CBA=∠CAB，

又∵∠ACB=90°，

∴∠CBA=∠CAB=45°，

又∵∠CAD=∠CBD=15°，

∴∠DBA=∠DAB=30°，

∴∠BDE=30°+30°=60°，

∵AC=BC，∠CAD=∠CBD=15°，

∴BD=AD，

在△ADC和△BDC中，

，

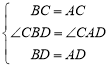∴△ADC≌△BDC（SAS），

∴∠ACD=∠BCD=45°，

∴∠CDE=60°，

∵∠CDE=∠BDE=60°，

∴DE平分∠BDC；

②解：结论：ME=BD，

理由：连接MC，

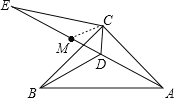
∵DC=DM，∠CDE=60°，

∴△MCD为等边三角形，

∴CM=CD，

∵EC=CA，∠EMC=120°，

∴∠ECM=∠BCD=45°

在△BDC和△EMC中，

，

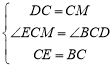∴△BDC≌△EMC（SAS），

∴ME=BD．