题目内容
【题目】写出命题“等腰三角形底边上的高线与顶角平分线重合”的逆命题,这个逆命题是真命题吗?请证明你的结论
【答案】逆命题:有一条边上的高线和这条边的对角平分线重合的三角形是等腰三角形,为真命题,证明见解析.
【解析】试题分析:根据逆命题的相关知识可将命题的题设和结论交换位置得到逆命题,然后利用三角形全等的判定和性质进行证明即可.
试题解析:逆命题:有一条边上的高线和这条边的对角平分线重合的三角形是等腰三角形
这个命题是真命题.
已知:如图,在△ABC中,AD⊥BC,且AD平分∠BAC.求证:三角形ABC是等腰三角形
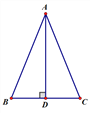
证明:∵AD⊥BC
∴ ∠BDA=∠CDA,
∵AD平分∠BA,
∴∠DAB=∠DAC,
在△ABD和△ACD中,
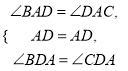
∴△ABD≌△ACD(ASA)
∴AB=AC,
∴△ABC是等腰三角形.

练习册系列答案
相关题目