题目内容
已知:如图,在△ABC中,∠ABC=90º,BD⊥AC于点D,点E在BC的延长线上,且BE=AB,过点E作EF⊥BE,与BD的延长线交于点F.求证:BC="EF" . 

根据同角的余角相等可得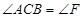 ,再结合∠ABC=90º,BD⊥AC,且BE=AB,即可根据“AAS”证得
,再结合∠ABC=90º,BD⊥AC,且BE=AB,即可根据“AAS”证得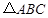

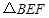 ,问题得证.
,问题得证.
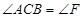 ,再结合∠ABC=90º,BD⊥AC,且BE=AB,即可根据“AAS”证得
,再结合∠ABC=90º,BD⊥AC,且BE=AB,即可根据“AAS”证得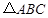

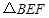 ,问题得证.
,问题得证.试题分析:∵
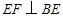 ,
,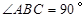 ,
,∴
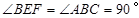
∴
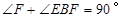 .
.又∵
 ,
,∴
 .
. ∴
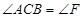
在
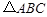 和
和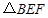 中,
中,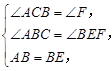
∴
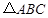

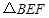
∴
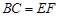 .
.点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
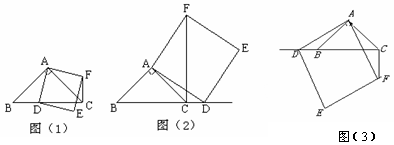
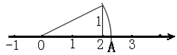

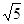
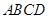 ,
,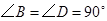 ,把纸片按如图所示折叠,使点
,把纸片按如图所示折叠,使点 落在
落在 边上的
边上的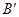 点,
点, 是折痕.
是折痕.
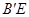 与
与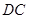 的位置关系;
的位置关系;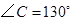 ,求
,求 的度数.
的度数.
