题目内容
【题目】如图,直线l:y=﹣2x+m与x轴交于点A(﹣2,0),抛物线C1:y=x2+4x+3与x轴的一个交点为B(点B在点A的左侧),过点B作BD垂直x轴交直线l于点 D.
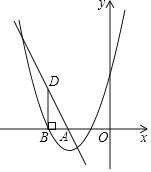
(1)求m的值和点B的坐标;
(2)将△ABD绕点A顺时针旋转90°,点B,D的对应点分别为点E,F.
①点F的坐标为 ;
②将抛物线C1向右平移使它经过点F,此时得到的抛物线记为C2,直接写出抛物线C2的表达式.
【答案】(1)m=﹣4,点B的坐标为(﹣3,0);(2)①(0,1);②y=x2﹣2![]() x+1或y=x2+2
x+1或y=x2+2![]() x+1.
x+1.
【解析】
(1)由点A的坐标,利用待定系数法即可求出m的值,再利用二次函数图象上点的坐标特征结合点B在点A的左侧,即可求出点B的坐标;
(2)利用一次函数图象上点的坐标特征可得出点D的坐标,进而可得出BD,AB的值.
①依照题意画出图形,由EF=BD=2,OF=AE=AB=1可得出点F在y轴正半轴上,进而可求出点F的坐标;
②利用配方程法将抛物线C1的表达式变形为顶点式,根据平移的性质可设抛物线C2的表达式为y=(x+m)2﹣1,由点F的坐标,利用待定系数法即可求出抛物线C2的表达式,此题得解.
解:(1)将A(﹣2,0)代入y=﹣2x+m,得:0=﹣2×(﹣2)+m,
解得:m=﹣4.
当y=0时,有x2+4x+3=0,
解得:x1=﹣3,x2=﹣1,
又∵点B在点A的左侧,
∴点B的坐标为(﹣3,0).
(2)当x=﹣3时,y=﹣2x﹣4=2,
∴点D的坐标为(﹣3,2),
∴BD=2,AB=1.
①依照题意画出图形,则EF=BD=2,OF=AE=AB=1,
又∵点A的坐标为(﹣2,0),
∴点F在y轴正半轴上,
∴点F的坐标为(0,1).
②∵y=x2+4x+3=(x+2)2﹣1,
∴设平移后得到的抛物线C2的表达式为y=(x+m)2﹣1.
将F(0,1)代入y=(x+m)2﹣1,得:1=(0+m)2﹣1,
解得:m1=![]() ,m2=﹣
,m2=﹣![]() ,
,
∴抛物线C2的表达式为y=(x﹣![]() )2﹣1或y=(x+
)2﹣1或y=(x+![]() )2﹣1,即y=x2﹣2
)2﹣1,即y=x2﹣2![]() x+1或y=x2+2
x+1或y=x2+2![]() x+1.
x+1.