题目内容
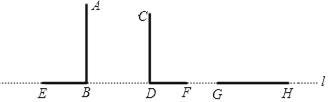
【题目】在同一水平线l上的两根竹竿AB、CD,它们在同一灯光下的影子分别为BE、DF,如图所示:(竹竿都垂直于水平线l)
(1)根据灯光下的影子确定光源S的位置;
(2)画出影子为GH的竹竿MG(用线段表示);
(3)若在点H观测到光源S的仰角是∠α,且 cosα=![]() ,GH=1.2m,请求出竹竿MG的长度.
,GH=1.2m,请求出竹竿MG的长度.
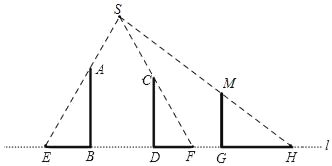
【答案】(1)如图见解析;(2)如图见解析;(3)竹杆MG的长度为0.9m.
【解析】
(1)过影子顶端与竹竿顶端作射线,交点S即为所求;
(2)连接光源S与影子顶端H,过G作垂直于地面的直线,与SH交于点M,GM即为所求;
(3)求得MH=1.5m,依据Rt△MHG中,∠MGH=90°,可得MG2=MH2﹣GH2=0.81,即可得到MG=0.9m
(1)如图,点S即为所求;
(2)如图,MG即为所求;
(3)∵cosα=![]() =
=![]() ,GH=1.2m,
,GH=1.2m,
∴MH=1.5m,
在Rt△MHG中,∠MGH=90°,
则MG2=MH2﹣GH2=0.81,
则MG=0.9m,
答:竹杆MG的长度为0.9m.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目