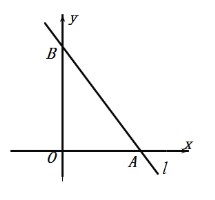题目内容
【题目】一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(﹣2,n)两点.
的图象交于A(1,4),B(﹣2,n)两点.
(1)求m和n的值;
(2)求k和b的值;
(3)结合图象直接写出不等式![]() -kx﹣b>0的解集.
-kx﹣b>0的解集.
【答案】(1)m= 4,n=﹣2;(2)k= 2,b= 2;(3)x<﹣2或0<x<1.
【解析】
(1)利用待定系数法把A和B的坐标代入即可求出m和n的值.
(2)A和B都在一次函数的图象上,所以把A和B的坐标代入得到关于k和b的一元二次方程,即可求得k和b的值.
(3)从图象可以看出函数y=![]() 的图象在y=kx+b的图象的上方的x的取值范围.就是不等式的解集.
的图象在y=kx+b的图象的上方的x的取值范围.就是不等式的解集.
(1)∵反比例函数y=![]() 的图象过点A(1,4),B(﹣2,n)两点,
的图象过点A(1,4),B(﹣2,n)两点,
∴![]() ,得m=4,
,得m=4,
∴n=![]() ,得n=﹣2,
,得n=﹣2,
即m的值是4,n的值是﹣2;
(2)∵一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(﹣2,﹣2)两点,
的图象交于A(1,4),B(﹣2,﹣2)两点,
∴![]() ,得
,得![]() ,
,
即k的值是2,b的值是2;
(3)由图象可知,
![]() kx﹣b>0
kx﹣b>0
不等式![]() kx﹣b>0的解集是x<﹣2或0<x<1.
kx﹣b>0的解集是x<﹣2或0<x<1.

练习册系列答案
相关题目
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2