题目内容
【题目】已知:△ABC内接于⊙0,连接AO并延长交BC于点D.

(l)如图l,求证:∠ABC+∠CAD=90°;
(2)如图2,过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE;
(3)如图3,在(2)的条件下,连接BO交DE于点F,延长ED交⊙0于点G,连接AG,若AC=![]() ,BF=OD,求线段AG的长.
,BF=OD,求线段AG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)线段AG的长为![]()
【解析】试题分析:(1)延长AD交⊙O于点M,连接MC,由AM为⊙O的直径得∠ACM=90°,所以∠AMC+∠MAC=90°,根据∠ABC和∠AMC是同弧的所对的角,则有∠ABC=∠AMC,从而得到∠B+∠CAD=90°;(2)过点O作OH⊥AC于H,连接BO,由![]() =
=![]() 得到∠AOB=2∠ACB,又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,∠BOD=∠BDO ,BD=BO 又因为∠BED=∠AHO 、∠ABD=∠AOH,所以△BDE≌△AOH,所以DE=AH ,又因为OH⊥AC ,AH=CH=
得到∠AOB=2∠ACB,又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,∠BOD=∠BDO ,BD=BO 又因为∠BED=∠AHO 、∠ABD=∠AOH,所以△BDE≌△AOH,所以DE=AH ,又因为OH⊥AC ,AH=CH=![]() AC ,所以AC=2DE ;(3)过点O作ON⊥EG于N, OT⊥AB于T连接OG, 因为
AC ,所以AC=2DE ;(3)过点O作ON⊥EG于N, OT⊥AB于T连接OG, 因为![]() ,所以DE=
,所以DE=![]() ,又因为OA=OB,所以∠ABO=∠BAO,因为∠ABO+∠BFE=90° ∠BAO+∠ADE=90°,所以∠BFE=∠OFD=∠ODF ,所以OF=OD ,因为BF=OD ,所以OF=OD=BF,所以△BFE≌△OFN ,所以BE=ON EF=FN,又因为OF=OD ON⊥FD,所以EF=FN=ND=
,又因为OA=OB,所以∠ABO=∠BAO,因为∠ABO+∠BFE=90° ∠BAO+∠ADE=90°,所以∠BFE=∠OFD=∠ODF ,所以OF=OD ,因为BF=OD ,所以OF=OD=BF,所以△BFE≌△OFN ,所以BE=ON EF=FN,又因为OF=OD ON⊥FD,所以EF=FN=ND=![]() ,因为BE=ON OG=BD ,所以△BED≌△NOG,所以ED=NG ,所以EG=
,因为BE=ON OG=BD ,所以△BED≌△NOG,所以ED=NG ,所以EG= ![]() ,又因为ON⊥EG OT⊥AB DE⊥AB ,所以四边形ONET为矩形 ,所以BE=ET=ON,因为OT⊥AB ,所以AT=BT AE=3BE,设AO=BD=r OD=
,又因为ON⊥EG OT⊥AB DE⊥AB ,所以四边形ONET为矩形 ,所以BE=ET=ON,因为OT⊥AB ,所以AT=BT AE=3BE,设AO=BD=r OD=![]() r AD=
r AD=![]() r,因为在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2,则可求出AE=15 ,在△AEG中由勾股定理得AG=
r,因为在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2,则可求出AE=15 ,在△AEG中由勾股定理得AG=![]()
![]()
 或r=-
或r=-![]() (舍去) AE=15 ,在△AEG中由勾股定理得AG=
(舍去) AE=15 ,在△AEG中由勾股定理得AG=![]()
试题解析:
(1)证明:延长AD交⊙O于点M,连接MC,如图所示:

∵AM为⊙O的直径,
∴∠ACM=90°
∴∠AMC+∠MAC=90°
∵![]() =
=![]()
∴∠ABC=∠AMC
∵∠AMC+∠MAC=90° (已证)
∴∠B+∠CAD=90°。
(2) 证明:过点O作OH⊥AC于H,连接BO,如图所示:

∵![]() =
=![]()
∴∠AOB=2∠ACB
∵∠ADC=2∠ACB
∴∠AOB=∠ADC
∴∠BOD=∠BDO
∴BD=BO
∵∠BED=∠AHO ∠ABD=∠AOH
∴△BDE≌△AOH
∴DE=AH
∵OH⊥AC
∴AH=CH=![]() AC
AC
∴AC=2DE
(3) 证明:过点O作ON⊥EG于N, OT⊥AB于T连接OG,如图所示:

∵![]()
∴DE=![]()
∵OA=OB
∴∠ABO=∠BAO
∵∠ABO+∠BFE=90° ∠BAO+∠ADE=90°
∴∠BFE=∠OFD=∠ODF
∴OF=OD
∵BF=OD
∴OF=OD=BF
∴△BFE≌△OFN
∴BE=ON EF=FN
∵OF=OD ON⊥FD
∴EF=FN=ND=![]()
∵BE=ON OG=BD
∴△BED≌△NOG
∴ED=NG
∴EG= ![]()
∵ON⊥EG OT⊥AB DE⊥AB
∴四边形ONET为矩形
∴BE=ET=ON
∵OT⊥AB
∴AT=BT AE=3BE
设AO=BD=r OD=![]() r AD=
r AD=![]() r
r
在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2
即![]()

![]() 或r=-
或r=-![]() (舍去) AE=15
(舍去) AE=15
在△AEG中由勾股定理得AG=![]()

【题目】下面的图形是由边长为1的正方形按照某种规律排列而组成的.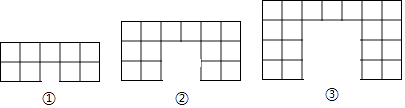
(1)观察图形,填写下表:
图形个数(n) | ① | ② | ③ |
正方形的个数 | 9 | ||
图形的周长 | 16 |
(2)推测第n个图形中,正方形的个数为 , 周长为(都用含n的代数式表示).
(3)写出第2016个图形的周长.