��Ŀ����
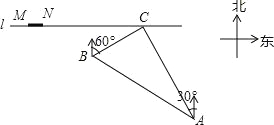
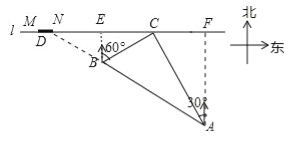
����Ŀ����ͼ����һ����ֱ�Ķ�������l����һ��Ϊ1.5km����ͷMN�͵���C������C����ͷ�Ķ���N��20km�����ִ���36km/h���ٶȺ��У�����10��00��A����õ���Cλ���ִ��ı�ƫ��30�㷽������10��40��B����õ���Cλ���ִ��ı�ƫ��60�㷽���������C���12km��
��1�����ִ��մ��ٶ��뺽����ʱ���ﺣ���ߣ�
��2�����ִ����ı亽���ִ��ܷ�ͣ������ͷ����˵�����ɣ����ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��
���𰸡���1���ִ��մ��ٶ��뺽��������11����00���ﺣ���ߣ���2���ִ����ı亽���ִ�����ͣ������ͷ�������������.
��������
���������(1���ӳ�AB��������l�ڵ�D������B��BE��������l�ڵ�E������A��AF��l��F����֤��ABC��ֱ�������Σ���֤����BAC=30���������BD�ij����ɽ�����⣮��2����RT��BEC�У����CD�ij��ȣ���CN��CM�Ƚϼ��ɽ�����⣮
�����������1���ӳ�AB��������l�ڵ�D������B��BE��������l�ڵ�E������A��AF��l��F����ͼ��ʾ��
�ߡ�BEC=��AFC=90������EBC=60������CAF=30����
���ECB=30������ACF=60����
���BCA=90����
��BC=12��AB=36��![]() =24��
=24��
��AB=2BC��
���BAC=30������ABC=60����
�ߡ�ABC=��BDC+��BCD=60����
���BDC=��BCD=30����
��BD=BC=12��
��ʱ��t=![]() =
=![]() Сʱ=20���ӣ�
Сʱ=20���ӣ�
���ִ��մ��ٶ��뺽��������11����00���ﺣ���ߣ�
��2����BD=BC��BE��CD��
��DE=EC��
��RT��BEC����BC=12����BCE=30����
��BE=6��EC=6![]() ��10.2��
��10.2��
��CD=20.4��
��20��20.4��21.5��
���ִ����ı亽���ִ�����ͣ������ͷ��

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�