题目内容
【题目】一个口袋中有1个黑球和若干个白球，这些球除颜色外其他都相同．已知从中任意摸取一个球，摸得黑球的概率为
．
（1）求口袋中白球的个数；
（2）如果先随机从口袋中摸出一球，不放回，然后再摸出一球，求两次摸出的球都是白球的概率．用列表法或画树状图法加以说明．
【答案】解：（1）∵一个口袋中有1个黑球和若干个白球，从中任意摸取一个球，摸得黑球的概率为
．
∴假设白球有x个，
∴
=，
∴x=2．
∴口袋中白球的个数为2个；
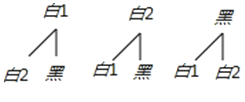
（2）∵先随机从口袋中摸出一球，不放回，然后再摸出一球，求两次摸出的球都是白球的概率．
∴两次都摸到白球的概率为：．
【解析】（1）根据摸得黑球的概率为 ， 假设出白球个数直接得出答案；
（2）利用先随机从口袋中摸出一球，不放回，得出树状图即可．
【考点精析】根据题目的已知条件，利用列表法与树状图法的相关知识可以得到问题的答案，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．
练习册系列答案
相关题目
【题目】将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3，图3中共有7个正方形；将图3中4个较小的正方形中的一个剪开得到图4，则图4中共有10个正方形，照这个规律剪下去：
（1）根据图中的规律补全表：
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
（2）第n个图形中有多少个正方形？
（3）当n=673时，图形中有多少个正方形？
