题目内容
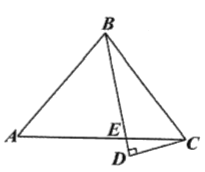
【题目】如图,![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,
,![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,则边
,则边![]() 的长为_____.
的长为_____.
【答案】![]()
【解析】
如图,延长BD到点G,使DG=BD,连接CG,则由线段垂直平分线的性质可得CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,根据等腰三角形的性质和三角形的内角和定理可得∠EFC=∠A=2∠CBE,再根据三角形的外角性质和等腰三角形的判定可得FC=FG,设CE=EF=x,则可根据线段间的和差关系求出DF的长,进而可求出FC的长,然后根据勾股定理即可求出CD的长,再一次运用勾股定理即可求出答案.
解:如图,延长BD到点G,使DG=BD,连接CG,则CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,
∵EA=EB,∴∠A=∠EBA,
∵∠AEB=∠CEF,
∴∠EFC=∠A=2∠CBE=2∠G,
∵∠EFC=∠G+∠FCG,
∴∠G=∠FCG,
∴FC=FG,
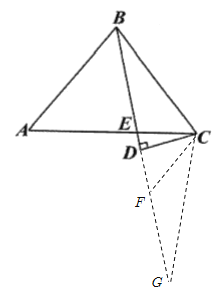
设CE=EF=x,则AE=BE=11-x,
∴DE=8-(11-x)=x-3,
∴DF=x-(x-3)=3,
∵DG=DB=8,
∴FG=5,∴CF=5,
在Rt△CDF中,根据勾股定理,得![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目