题目内容
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
【答案】(1)b=2,c=1. 顶点所在的格点为E.(2)F点在该抛物线上,H点不在该抛物线上.(3)8.
【解析】试题分析:(1)根据-1的奇数次方等于-1,再把点H、C的坐标代入抛物线解析式计算即可求出b、c的值,然后把函数解析式整理成顶点式形式,写出顶点坐标即可;
(2)根据-1的偶数次方等于1,再把点A、B的坐标代入抛物线解析式计算即可求出b、c的值,从而得到函数解析式,再根据抛物线上点的坐标特征进行判断;
(3)分别利用(1)(2)中的结论,将抛物线平移,可以确定抛物线的条数.
试题解析:(1)n为奇数时,y=-x2+bx+c,
∵l经过点H(0,1)和C(2,1),
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=-x2+2x+1,
y=-(x-1)2+2,
∴顶点为格点E(1,2);
(2)n为偶数时,y=x2+bx+c,
∵l经过点A(1,0)和B(2,0),
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=x2-3x+2,
当x=0时,y=2,
∴点F(0,2)在抛物线上,点H(0,1)不在抛物线上;
(3)所有满足条件的抛物线共有8条.
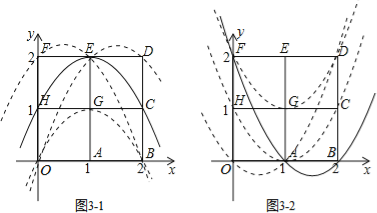
当n为奇数时,由(1)中的抛物线平移又得到3条抛物线,如答图3-1所示;
当n为偶数时,由(2)中的抛物线平移又得到3条抛物线,如答图3-2所示.