题目内容
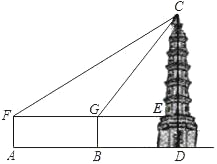
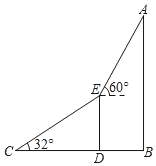
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】(1)248米(2)594米
【解析】
(1)在Rt△DCE中,根据正切函数的定义即可求出大厦DE的高度;
(2)作EF⊥AB于F.由题意,得EF=DB=200米,BF=DE,∠AEF=60°.在Rt△AFE中,根据正切函数的定义得出AF=EFtan∠AEF,由AB=BF+AF即可得到结论.
(1)∵在Rt△DCE中,∠CDE=90°,∠ECD=32°,CD=400,∴DE=CDtan∠ECD≈400×0.62=248(米).
答:大厦DE的高度约为248米.
(2)如图,作EF⊥AB于F.
由题意,得:EF=DB=200,BF=DE=248,∠AEF=60°.
在Rt△AFE中,∵∠AFE=90°,∴AF=EFtan∠AEF≈200×1.73=346,∴AB=BF+AF=248+346=594(米).
答:平安金融中心AB的高度约为594米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目