题目内容
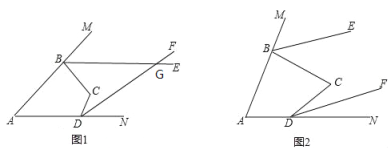
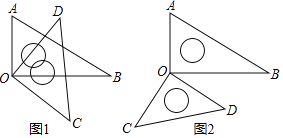
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图1,若∠BOD=25°,则∠AOC= °;若∠AOC=125°,则∠BOD= °;
(2)如图2,若∠BOD=50°,则∠AOC= °;若∠AOC=140°,则∠BOD= °;
(3)猜想∠AOC与∠BOD的大小关系: ;并结合图(1)说明理由.
【答案】(1)155,55;(2)130,40;(3)∠AOC与∠BOD互补,理由见解析.
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD﹣∠BOD可分别计算出∠AOC、∠BOD的度数;
(2)根据∠AOC=∠AOB+∠COD﹣∠BOD计算可得;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180![]() 且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
解:(1)若∠BOD=25![]() ,
,
∵∠AOB=∠COD=90![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣25
﹣25![]() =155
=155![]() ,
,
若∠AOC=125![]() ,
,
则∠BOD=∠AOB+∠COD﹣∠AOC=90![]() +90
+90![]() ﹣125
﹣125![]() =55
=55![]() ;
;
故答案为:155,55.
(2)若∠BOD=50![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣50
﹣50![]() =130
=130![]() ,
,
若∠AOC=140![]() ,
,
则∠BOD=360![]() ﹣∠AOC﹣∠AOB﹣∠COD=40
﹣∠AOC﹣∠AOB﹣∠COD=40![]() ;
;
故答案为:130,40.
(3)∠AOC与∠BOD互补.
∵∠AOD+∠BOD+∠BOD+∠BOC=180![]() ,∠AOD+∠BOD+∠BOC=∠AOC,
,∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180![]() ,
,
即∠AOC与∠BOD互补.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】某公司在![]() 两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从
两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从![]() 地运一台到甲、乙两地的费用分别是500元和400元;从
地运一台到甲、乙两地的费用分别是500元和400元;从![]() 地运一台到甲、乙两地费用分别是300元和600元,设从
地运一台到甲、乙两地费用分别是300元和600元,设从![]() 地运往甲地
地运往甲地![]() 台挖掘机.
台挖掘机.
(1)请补全下表,并求出运这批挖掘机的总费用是多少?
甲 | 乙 | 总计 | |
|
| ____________台 | 16台 |
| _______________台 | ____________台 | 12台 |
总计 | 15台 | 13台 | 28台 |
(2)当从![]() 地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
(3)怎样安排运输方案,可使运这批挖掘机的总费用最少,最少费用是多少?