МвДҝДЪИЭ
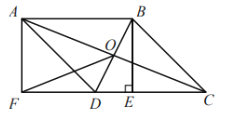
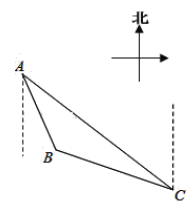
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCКЗС§ЙъРЎҪрјТёҪҪьөДТ»ҝйИэҪЗРОВМ»ҜЗшөДКҫТвНјЈ¬ОӘФцЗҝМеЦКЈ¬ЛыГҝМмФзіҝ¶јСШЧЕВМ»ҜЗшЦЬұЯРЎВ·ABЎўBCЎўCAЕЬІҪЈЁРЎВ·өДҝн¶ИІ»јЖЈ©Ј®№ЫІвөГөгBФЪөгAөДДПЖ«¶«30Ўг·ҪПтЙПЈ¬өгCФЪөгAөДДПЖ«¶«60ЎгөД·ҪПтЙПЈ¬өгBФЪөгCөДұұЖ«Оч75Ўг·ҪПтЙПЈ¬ACјдҫаАлОӘ600ГЧЈ®ОКРЎҪрСШИэҪЗРОВМ»ҜЗшөДЦЬұЯРЎВ·ЕЬТ»ИҰ№ІЕЬБЛ¶аЙЩГЧЈҝЈЁҪб№ыұЈБфёщәЕЈ¬УСЗйМбКҫЈә№эөгCЧцёЁЦъПЯЈ¬№№ФмЦұҪЗИэҪЗРОЈ©
Ўҫҙр°ёЎҝ(300+300![]() +300
+300![]() )ГЧ
)ГЧ
ЎҫҪвОцЎҝ
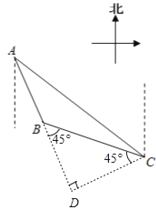
№эөгCЧчCDЎНABҪ»ABСУіӨПЯУЪТ»өгDЈ¬ёщҫЭМвТвөГЎПBACЈҪ30ЎгЈ¬ЎПBCAЈҪ15ЎгЈ¬АыУГИэҪЗРОөДНвҪЗөДРФЦКөГөҪЎПDBCЈҪЎПDCBЈҪ45ЎгЈ¬И»әуФЪRtЎчADCЦРЈ¬ЗуөГCDЈҪBDЈҪ300ГЧәујҙҝЙЗуөГBCәНABөДіӨЈ¬№КҝЙөГИэҪЗРОABCөДЦЬіӨЈ®
ҪвЈә№эөгCЧчCDЎНABҪ»ABСУіӨПЯУЪТ»өгDЈ¬
ЎЯөгBФЪөгAөДДПЖ«¶«30Ўг·ҪПтЙПЈ¬өгCФЪөгAөДДПЖ«¶«60ЎгөД·ҪПтЙПЈ¬өгBФЪөгCөДұұЖ«Оч75Ўг·ҪПтЙПЈ¬
ЎаЎПBACЈҪ30ЎгЈ¬ЎПBCAЈҪ15ЎгЈ¬
№КЎПDBCЈҪЎПDCBЈҪ45ЎгЈ¬
ФЪRtЎчADCЦРЈ¬
ЎЯACЈҪ600ГЧЈ¬ЎПBACЈҪ30ЎгЈ¬
ЎаCDЈҪBDЈҪ300ГЧЈ¬
ЎаBCЈҪCDЎВsin45Ўг=300![]() ГЧЈ¬ADЈҪCDЎВtan30Ўг=300
ГЧЈ¬ADЈҪCDЎВtan30Ўг=300![]() ГЧ
ГЧ
ЎаABЈҪADBDЈҪЈЁ300![]() 300Ј©ГЧЈ¬
300Ј©ГЧЈ¬
ЎаИэҪЗРОABCөДЦЬіӨОӘAC+AB+BC=600Ј«ЈЁ300![]() 300Ј©+300
300Ј©+300![]() =300+300
=300+300![]() +300
+300![]() (ГЧ)
(ГЧ)
ҙрЈәРЎҪрСШИэҪЗРОВМ»ҜЗшөДЦЬұЯРЎВ·ЕЬТ»ИҰ№ІЕЬБЛФј(300+300![]() +300
+300![]() )ГЧЈ®
)ГЧЈ®