题目内容
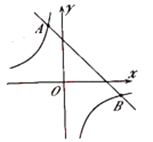
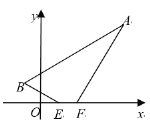
【题目】如图,在直角坐标系中,已知A(4,4),B(-1,1),EF=1,线段EF在x轴上平移,当四边形ABEF的周长最小时,点E坐标是__________.
【答案】![]()
【解析】
欲使四边形ABEF的周长最小,由于线段AB与EF是定长,所以只需BE+AF最小.为此,先确定点E、F的位置:过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则点E、F的位置确定.再根据待定系数法求出直线A′B′的解析式,然后令y=0,即可求出点E的横坐标,进而得出点E的坐标.
如图,过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则此时四边形ABEF的周长最小.
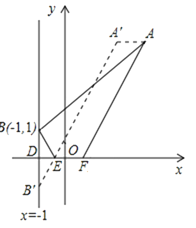
∵A(4,4),
∴A′(3,4),
∵B(-1,1),
∴B′(-1,-1).
设直线A′B′的解析式为y=kx+b,
则![]() ,
,
解得![]() .
.
∴直线A′B′的解析式为y=![]() ,
,
当y=0时,![]() =0,解得x=-
=0,解得x=-![]() .
.
故线段EF平移至如图2所示位置时,四边形ABEF的周长最小,此时点E的坐标为(-![]() ,0).
,0).
故答案为:(-![]() ,0).
,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目