ЬтФПФкШн
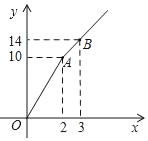
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНkxЉ2kЃЈkЃМ0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌABЃН2![]() ЃЎ
ЃЎ

ЃЈ1ЃЉжБНгаДГіЕуAЃЌЕуBЕФзјБъЃЛ
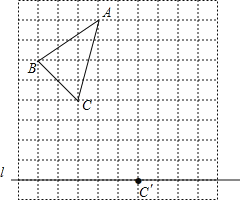
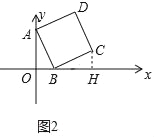
ЃЈ2ЃЉШчЭМ2ЃЌвдABЮЊБпЃЌдкЕквЛЯѓЯоФкЛГіе§ЗНаЮABCDЃЌЧѓжБЯпDCЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЃЈ2ЃЉжае§ЗНаЮABCDЕФЖдНЧЯпACЁЂBDМДНЛгкЕуGЃЌКЏЪ§yЃНmxКЭyЃН![]() ЃЈxЁй0ЃЉЕФЭМЯѓОљОЙ§ЕуGЃЌЧыРћгУетСНИіКЏЪ§ЕФЭМЯѓЃЌЕБmxЃО
ЃЈxЁй0ЃЉЕФЭМЯѓОљОЙ§ЕуGЃЌЧыРћгУетСНИіКЏЪ§ЕФЭМЯѓЃЌЕБmxЃО![]() ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ0ЃЌ4ЃЉЃЌBЃЈ2ЃЌ0ЃЉ;ЃЈ2ЃЉyЃНЉ2x+14;ЃЈ3ЃЉЉ3ЃМxЃМ0ЛђxЃО3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжБЯпЕФНтЮіЪНгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌЗжБ№АбЕуAКЭЕуBгУКЌгаkЕФДњЪ§ЪНБэЪОГіРДЃЌдйИљОнAB=2![]() ЧѓГіkМДПЩЕУAЁЂBЕФзјБъЃЛ
ЧѓГіkМДПЩЕУAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉзїCHЁЭxжсгкHЃЌИљОне§ЗНаЮЕФаджЪКЭШЋЕШШ§НЧаЮЕФХаЖЈЯШЧѓжЄЁїAOBЁеЁїBHCЃЌДгЖјЕУЕНCHЃН2ЃЌBHЃН4ЃЌНјЖјЕУЕНЕуCЕФзјБъЃЌдйИљОнЦНааЯпЕФаджЪЧѓГіжБЯпCDЕФНтЮіЪНМДПЩЃЛ
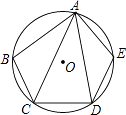
ЃЈ3ЃЉЯШЧѓГідкЕквЛЯѓЯоФкНЛЕуЕФзјБъЃЌИљОнКЏЪ§ЕФаджЪКЭЭМЯѓЙлВьМДПЩЕУ.
НтЃКЃЈ1ЃЉЁпжБЯпyЃНkxЉ2kЃЈkЃМ0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌ
ЁрAЃЈ0ЃЌЉ2kЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЁпABЃН2![]() ЃЌ
ЃЌ
Ёр4+4k2ЃН20ЃЌ
Ёрk2ЃН4ЃЌ
ЁпkЃМ0ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрAЃЈ0ЃЌ4ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзїCHЁЭxжсгкHЃЎ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрABЃНBCЃЌЁЯAOBЃНЁЯABCЃНЁЯBHCЃН90ЁуЃЌ
ЁрЁЯABO+ЁЯCBHЃН90ЁуЃЌЁЯCBH+ЁЯBCHЃН90ЁуЃЌ
ЁрЁЯABOЃНЁЯBCHЃЌ
ЁрЁїAOBЁеЁїBHCЃЌ
ЁрCHЃНOBЃН2ЃЌBHЃНOAЃН4ЃЌ
ЁрCЃЈ6ЃЌ2ЃЉЃЌ
ЁпCDЁЮABЃЌ
ЁрПЩвдМйЩшжБЯпCDЕФНтЮіЪНЮЊyЃНЉ2x+bЃЌАбCЃЈ6ЃЌ2ЃЉДњШыЕУЕНbЃН14ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊyЃНЉ2x+14ЃЎ
ЃЈ3ЃЉ
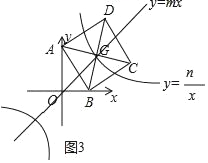
гЩAЁЂCзјБъЃЌПЩжЊдкЕквЛЯѓЯоФкНЛЕуДэБъЮЊЃЈ3,3ЃЉЙлВьЭМЯѓПЩжЊжБЯпyЃНmxгы yЃН![]() ЕФНЛЕузјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈЉ3ЃЌЉ3ЃЉЃЌ
ЕФНЛЕузјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈЉ3ЃЌЉ3ЃЉЃЌ
ЁрmxЃО![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЮЊЉ3ЃМxЃМ0ЛђxЃО3ЃЎ
ЪБЃЌxЕФШЁжЕЗЖЮЇЮЊЉ3ЃМxЃМ0ЛђxЃО3ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y1=aЃЈxЉ2ЃЉ2+kжаЃЌКЏЪ§y1гыздБфСПxЕФВПЗжЖдгІжЕШчБэЃК
x | Ё | 1 | 2 | 3 | 4 | Ё |
y | Ё | 2 | 1 | 2 | 5 | Ё |
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФБэДяЪНЃЛ