题目内容
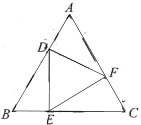
【题目】如图,等边![]() 的顶点分别在等边
的顶点分别在等边![]() 各边上,且
各边上,且![]() 于
于![]() ,若
,若![]() ,则
,则![]() _____.
_____.
【答案】![]()
【解析】
首先利用“AAS”证明△BED与△ADF及△CFE彼此全等,则AD=BE,然后再利用30°角所对的直角边等于斜边的一半求出BE=![]() BD,据此进一步求出BD=4,BE=2,最后利用勾股定理加以求解即可.
BD,据此进一步求出BD=4,BE=2,最后利用勾股定理加以求解即可.
∵△ABC与△DEF为等边三角形,
∴∠A=∠B=∠C=∠EDF=∠DFE=∠FED=60°,AB=AC=BC,DE=DF=EF,
∵![]() ,
,
∴∠BDE=90°60°=30°,
∴∠ADF=180°30°60°=90°,
同理可得:∠EFC=90°,
∴△BED△ADF△CFE(AAS),
∴AD=BE=CF,
在Rt△BDE中,
∵∠BDE=30°,
∴BE=![]() BD,
BD,
∵AB=BD+AD=BD+BE=![]() BD=6,
BD=6,
∴BD=4,
∴BE=AD=2,
∴在Rt△BDE中,![]() ,
,
故答案为:![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目