��Ŀ����
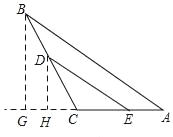
����Ŀ����1����ͼ1����ABC�У���CΪֱ�ǣ�AC=6��BC=8��D��E����ֱ��B��A��ʼͬʱ�������ֱ����߶�BC��AC��C�������˶�����C���ֹͣ�����ǵ��ٶȶ�Ϊÿ��1����λ������D�����2�����CDE�����Ϊ���٣�
��2����ͼ2������1���е���������CΪֱ������Ϊ��CΪ�۽ǣ������������䣬�����Ƿ���Ȼ����ijһʱ�̣�ʹ����CDE�����Ϊ��ABC�����һ�룿�����ڣ��������һʱ�̣��������ڣ���˵�����ɣ�
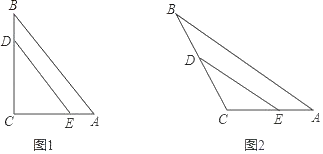
���𰸡���1��D�����2�����CDE�����Ϊ12����2��D�����2����ʱ��CDE�����Ϊ��ABC�����һ�룬���ɼ�����.
��������
��1��D��E����2���BD=AE=2��Ȼ�����CD��CE�ij������������ε������ʽ��⼴�ɣ�
��2����ͼ����B��D��ֱ���AC��CE���ϵĸߣ���D��E�˶�ʱ��Ϊx�룬���ݸ��������ε������ʽ�г�����ʽ��⼴��.
��1����D��E����2���BD=AE=2��
��CD=BC��BD=8��2=6��CE=AC��AE=6��2=4��
��S��CDE=![]() CD��CE=
CD��CE=![]() ��6��4=12.
��6��4=12.
��D�����2�����CDE�����Ϊ12.
��2����ͼ����B��D��AC���ϵĸ�DH��BG
��D��E�˶�ʱ��Ϊx�룬
��![]() (8��x)(6��x)sin��BCG=
(8��x)(6��x)sin��BCG=![]() ��6��8sin��BCG
��6��8sin��BCG
���x=2��x=12����ȥ����
����D�����2����ʱ��CDE�����Ϊ��ABC�����һ�룬