题目内容
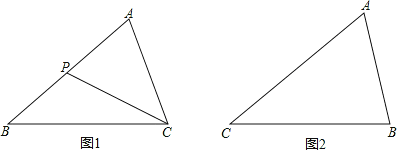
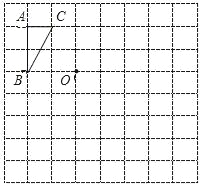
【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
【答案】(1)证明见解析;(2)证明见解析;(3)25:3.
【解析】
(1)利用ASA证明△APN≌△CPQ,可得AN=CQ;
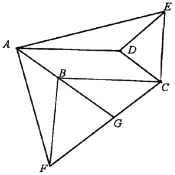
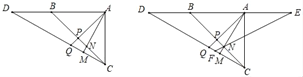
(2)如图2,连接BQ,证明△DBQ≌△EAN(SAS),可得DQ=EN;
(3)设AE=2x,AB=3x,则BD=2x,DC=![]() x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得
x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得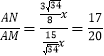 ,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,可得结论.
,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,可得结论.
解:(1)证明:∵∠APB=90°
∴∠APN=∠CPQ=90°,
∴∠PNA+∠NAP=∠NAP+∠CQP=90°,
∴∠PNA=∠CQP,
∵AB=AC,∠BAC=90°,
∴AP=PC,
∴△APN≌△CPQ(ASA),
∴AN=CQ;
(2)证明:如图2,连接BQ,
由(1)知:AP是BC的垂直平分线,
∴BQ=CQ,
∵AN=CQ,
∴AN=BQ,
∵BQ=CQ,
∴∠QBC=∠QCB=∠NAP,
∵∠PBA=∠PAB=45°,
∴∠QBA=∠BAN,
∴∠DBQ=∠NAE,
∵BD=AE,
∴△DBQ≌△EAN(SAS),
∴DQ=EN;
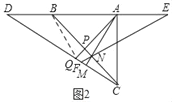
(3)∵3AE=2AB,
∴设AE=2x,AB=3x,则BD=2x,DC=![]() x,
x,
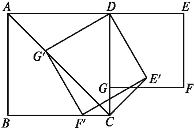
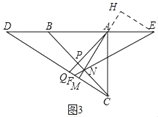
如图3,过E作EH⊥AM,交MA的延长线于H,
∴∠H=∠AMD=90°,
∴EH∥DC,
∴∠HEA=∠CDA,
∴△AHE∽△AMD,
∴![]() ,
,
∵∠MAC=∠CDA,∠ACN=∠DAQ=45°,
∴△DQA∽△ANC,
∴![]() ,
,
由(2)知:CQ=AN,
∴![]() ,
,
∴AN=CQ=![]() ,
,
S△ADC=![]() ,
,
![]() ,
,
AM=![]() ,
,
∴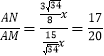 ,
,
∴设AH=8m,AM=20m,AN=17m,
则MN=3m,
∵EH∥FM,
∴△EHN∽△FMN,
∴![]() .
.
故答案为:25:3.

 名校课堂系列答案
名校课堂系列答案