题目内容
【题目】如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为___________

【答案】(2,3)
【解析】
过点C作CD⊥y轴于点D,通过角的计算可找出∠OAB=∠DBC,结合∠AOB=∠BDC、AB=BC,即可证出△OAB≌△DBC(AAS),根据全等三角形的性质即可得出BD=AO、DC=OB,再结合点A、B的坐标即可得出DC、OD的长度,进而可得出点C的坐标.
解:过点C作CD⊥y轴于点D,如图所示.
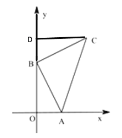
∵∠ABC=90°,∠AOB=90°,
∴∠OAB+∠OBA=90°,∠OBA+∠DBC=90°,
∴∠OAB=∠DBC.
在△OAB和△DBC中,
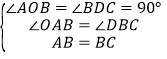 ,
,
∴△OAB≌△DBC(AAS),
∴BD=AO,DC=OB.
∵A(1,0)、B(0,2),
∴BD=AO=1,DC=OB=2,OD=OB+BD=3,
∴点C的坐标为(2,3).
故答案为:(2,3).

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目