题目内容
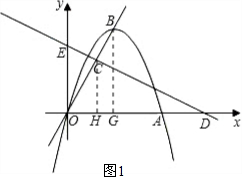
如图,在直角坐标平面内,O为原点,抛物线 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上.
(1)求m的值和抛物线 的解析式;
的解析式;
(2)如在线段OB上有一点C,满足 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.

 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上.(1)求m的值和抛物线
 的解析式;
的解析式;(2)如在线段OB上有一点C,满足
 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.

(1)3,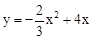 ;(2)①
;(2)①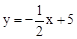 ;②(-5,
;②(-5,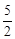 )或(4,8)或
)或(4,8)或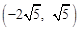 .
.
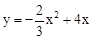 ;(2)①
;(2)①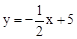 ;②(-5,
;②(-5,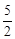 )或(4,8)或
)或(4,8)或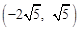 .
.试题分析:(1)先根据抛物线
 的顶点B(m,6)在直线
的顶点B(m,6)在直线 上可求出m的值,再用待定系数发即可求出此抛物线的解析式.
上可求出m的值,再用待定系数发即可求出此抛物线的解析式.(2)①作CH⊥OA,BG⊥OA,再根据平行线分线段成比例定理即可得出CH的长,进而求出C点坐标,再根据D点坐标用待定系数法即可求出直线DC解析式.
②根据菱形的性质即可求出符合条件的N点坐标.
(1)∵顶点B(m,6)在直线
 上,∴m="3." ∴B(3,6).
上,∴m="3." ∴B(3,6).把A、B两点坐标代入抛物线的解析式得,
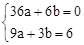 ,解得
,解得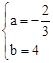 .
.∴抛物线的解析式为:
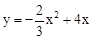 .
.(2)①如图1,作CH⊥OA,BG⊥OA,
∴CH∥BG,∴△OCH∽△OBG. ∴
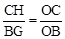 .
.∵OC=2CB,∴
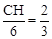 ,即CH="4." ∴点C的坐标为(2,4).
,即CH="4." ∴点C的坐标为(2,4).∵D(10,0),∴根据题意
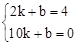 ,解得:
,解得: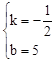 .
.∴直线DC解析式
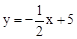 .
.
②如图2:∵四边形ENOM是菱形,∴OS=ES=
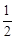 OE=
OE=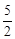 . ∴NK=
. ∴NK=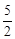 .
.∵ON∥DE,∴tan∠NOK=tan∠EDO=
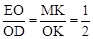 .∴OK=5.∴N1(-5,
.∴OK=5.∴N1(-5,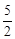 ).
).
如图3:∵EM⊥OB,∴ON=2OC.
∵点C的坐标为(2,4),∴N2(4,8).
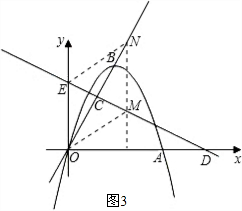
③如图4:∵直线DC解析式
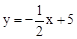 ,∴E(0,5).
,∴E(0,5).设M(x,
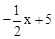 ),
),∵四边形ENOM是菱形,∴EM=OE=5,即
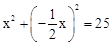 ,解得x=
,解得x=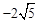 .∴M
.∴M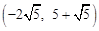 .
.∴可设N(
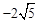 ,y),则
,y),则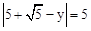 ,解得y=
,解得y=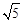 或y=
或y=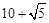 (舍去).∴N3
(舍去).∴N3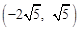 .
.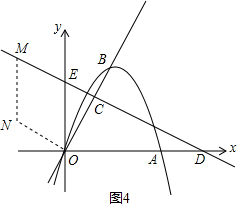
综上所述,点N的坐标为(-5,
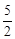 )或(4,8)或
)或(4,8)或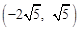 .
.
练习册系列答案
相关题目
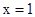 的抛物线的解析式 .
的抛物线的解析式 .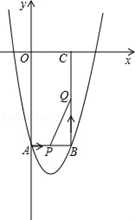

 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
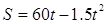 ,则飞机着陆后滑行 米才能停下来。
,则飞机着陆后滑行 米才能停下来。