Question

【题目】如图，在平面直角坐标系中，直线 与双曲线 交于、两点，已知点，点.

（1）求直线和双曲线的解析式；

（2）把直线沿轴负方向平移2个单位后得到直线，直线与双曲线交于、两点，当时，求的取值范围.

Answer 1

【答案】（1）∴直线和双曲线的解析式分别为：和；（2）的取值范围是：或.

【解析】

（1）把点B 代入双曲线求出a的值，即可得到双曲线的解析式；把点A代入双曲线求出m的值，确定A点坐标，再利用待定系数法求出直线的解析式，即可解答；

（2）先求出y3的解析式，再解方程组求出点D点E的坐标，即可解答．

（1）∵

又∵在双曲线上，即，

又∵点在双曲线上，即，即，，

∵，在直线上，

∴，解得，

∴直线和双曲线的解析式分别为：和.

（2）∵直线是直线沿轴负方向平移2个单位得到，

∴，

解方程组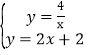：得，或

∴当，，

∴当时，的取值范围是：或.