题目内容
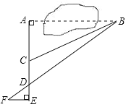
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.

【答案】(1)BC=2;(2)见解析;
【解析】试题分析:
(1)由已知条件根据“垂径定理”易得AP=CP=![]() AC=
AC=![]() ,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=
,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=![]() BC,由此可得BC=2;
BC,由此可得BC=2;
(2)由OG=9,OA=3,OB=3,OP=1,可得![]() ,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
试题解析:
(1)∵DE是⊙O的直径,且DE⊥AC,
∴AP=PC=![]() AC=
AC=![]() ,
,
又∵OA=3,
∴OP=1
又AB是⊙O的直径,
∴O为AB的中点,
∴OP=![]() BC,
BC,
∴BC=2OP=2.
(2)∵OG=9,OA=3,OB=3,OP=1,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∠BOG=∠POA,
∴△BOG∽△POA,
∴∠GBO=∠OPA=90°
又∵点B在⊙O上,
∴FG是⊙O的切线.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目